<ポイント>
PERT法とは仕事をスケジュール管理する方法です。
色々な作業がある中で「最終的な仕事の完了日」を求めることができます。
「各作業の中継地点までの所要日数」を書き込めばいいだけなので、とても対策しやすいカテゴリです!(*´∀`*)
【PERT法の基本】
PERT法が出題される場合は下記の説明と図が示されます。
このルールはどのPERT法の問題でも変わらないため、あらかじめ覚えておきましょう。
【ルール】
下図は、ある作業の手順とそれにかかる日数を示している。
ある作業を始めるためには、その作業の前にある矢印の作業が全て終わらなければならない。
また、次の作業は、前の作業が全て終わった日の翌日から始めることができる。
例えば、③の作業を始めるには②の作業が終わらなければならない。
また、④の作業を始めるには、①と③の作業が終わらなければならない。
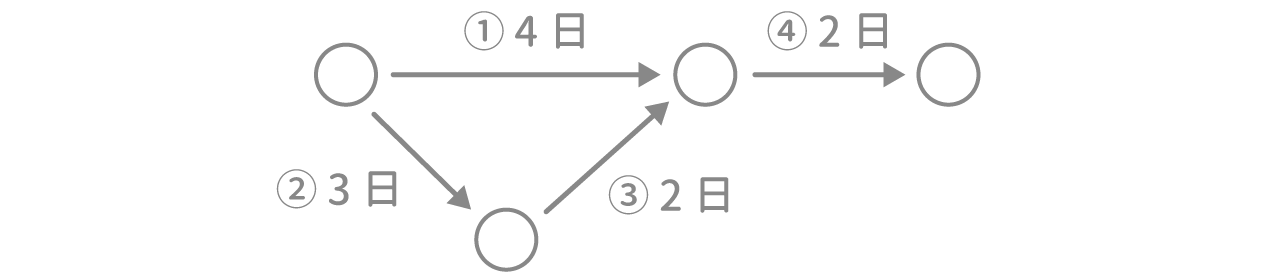
PERT法では仕事全体が最短で終わる日数を求めます。
中継地点にそこまでの所要日数をメモしてゆくのを、仕事の始まりから終わりまで、順番に繰り返すだけです!(*´∀`*)
![]()
<基本問題>
下図は、ある作業の手順とそれにかかる日数を示している。 ただし、①~⑩までの番号は作業の種類を識別するためのもので、この順番に作業が行われるという意味ではない。 ある作業を始めるためには、その作業の前に集まる矢印の作業が全て終わらなければならない。 また次の作業は、前の作業が全て終わった日の翌日から始めることができる。以下の問いに答えよ。
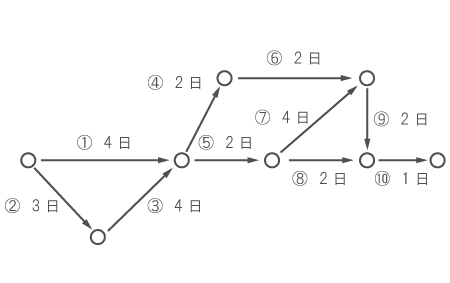
(1)⑦の作業を始めるためには、どの作業が終わっている必要があるか。
(2)全工程を全てやり終えるためには、最短で何日間かかるか。
(1) ⑦の作業を始めるには、⑤の作業が終わっていなければならない。 ⑤の作業を始めるには、①と③の作業が終わっていなければならない。 ③の作業を始めるには、②の作業が終わっていなければならない。
したがって、①②③⑤の作業が終わっている必要がある。
(2)
下図のように、○(中継地点)にそこまでの所要日数をメモしてゆくのを、仕事の始まりから終わりまで、順番に繰り返す。
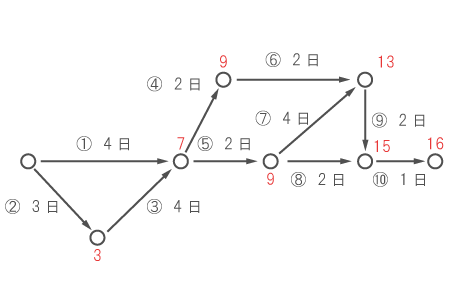
複数の矢印が集まる○の所要日数を求めるためには、「その地点の前の○までの所要日数 + その作業にかかる日数」を複数の矢印同士で比較して、最多のものをメモする。
例えば、作業⑨の前の13(最多所要日数)をメモするためには、作業⑥が終わった時点での所要日数である
- 式)9 + 2 = 11
と、作業⑦が終わった時点での所要日数である
- 式)9 + 4 = 13
を比較し、最多である13をメモする必要がある。
上図より、仕事が最短で終わる日数は16日である。
遅れてもよい日数
下図は、ある作業の手順とそれにかかる日数を示している。 ただし、①~⑫までの番号は作業の種類を識別するためのもので、この順番に作業が行われるという意味ではない。 ある作業を始めるためには、その作業の前に集まる矢印の作業が全て終わらなければならない。 また次の作業は、前の作業が全て終わった日の翌日から始めることができる。以下の問いに答えよ。
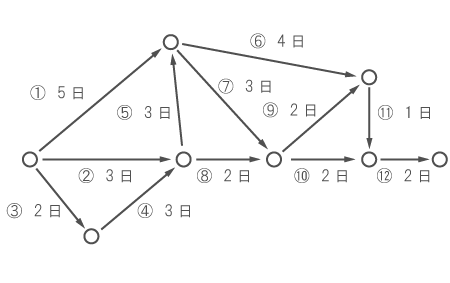
(1)⑥の作業と⑦の作業を予定通りの日程で始めたいとき、①の仕事は最大何日遅れてもよいか。ただし、①以外の作業は予定通りに進むものとする。
A→C3日
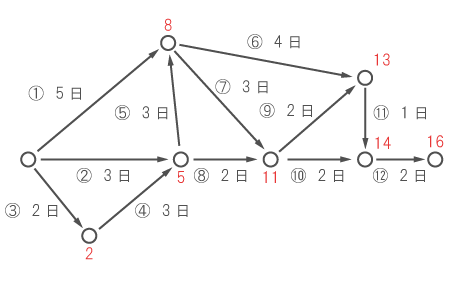
上図のように、○(中継地点)にそこまでの所要日数をメモしてゆくのを、仕事の始まりから終わりまで、順番に繰り返す。
図より、⑥と⑦の作業をするために必要な日数は8日である。
一方、①の作業は、仕事の始まりとなる作業で、そのまま⑥と⑦の作業に直結する。また、作業予定日数は5日である。
したがって、①の作業は
- 式)8 – 5 = 3(日)
遅れても⑥と⑦の作業は予定通り行うことができる。
仕事完了日
下図は、ある作業の手順とそれにかかる日数を示している。 ただし、①~⑫までの番号は作業の種類を識別するためのもので、この順番に作業が行われるという意味ではない。 ある作業を始めるためには、その作業の前に集まる矢印の作業が全て終わらなければならない。 また次の作業は、前の作業が全て終わった日の翌日から始めることができる。以下の問いに答えよ。
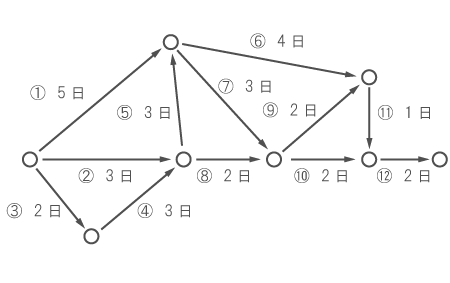
(2)全工程を全てやり終えるためには、最短で何日かかるか。
A→E16日
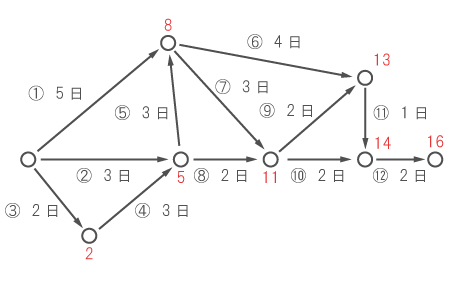
上図の通り、○(中継地点)までの最多所要日数を書き込む。
(2)上図の通り、○(中継地点)までの最多所要日数を書き込む。
仕事が最短で終わる日数は16日である。
遅れた場合の仕事完了日
下図は、ある作業の手順とそれにかかる日数を示している。 ただし、①~⑭までの番号は作業の種類を識別するためのもので、この順番に作業が行われるという意味ではない。 ある作業を始めるためには、その作業の前に集まる矢印の作業が全て終わらなければならない。 また次の作業は、前の作業が全て終わった日の翌日から始めることができる。以下の問いに答えよ。
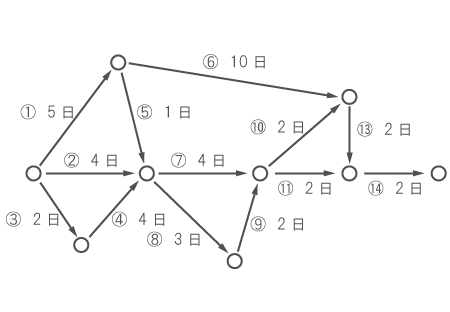
(2)⑨の作業が3日遅れてしまった。このとき、全工程を全てやり終えるためには、最短で何日かかるか。
⑨の作業は
- 式)2 + 3 = 5(日)
かかったことになる。
これを踏まえて、○(中継地点)までの最多所要日数を書き込む。
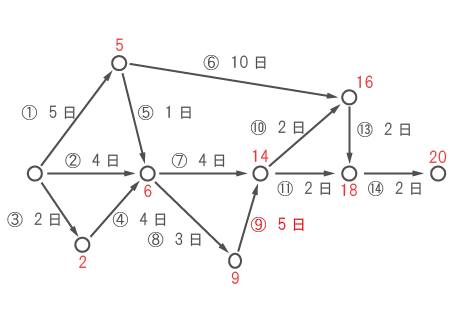
したがって、仕事が最短で終わる日数は20日である。
