<ポイント>
「列車が電柱を通過する」「列車が駅を通過する」「列車が他の列車とすれ違う」などの様々な状態において、所要時間が問われます。
どんなに複雑な状況であっても「列車の先頭に旗」でイメージがつかめるでしょう!(*´∀`*)
- 列車の最前部に「旗」を立て、旗がどれだけ移動したかに注目しよう!
- 速さに関する3公式を覚えておこう!
- 秒速 ⇔ 時速の変換公式を覚えておこう!
【速さに関する3公式】
- 公式① [ 距離 ] = [ 速さ ]×[ 時間 ]
- 公式② [ 速さ ] = [ 距離 ]÷[ 時間 ]
- 公式③ [ 時間 ] = [ 距離 ]÷[ 速さ ]
【秒速 ⇔ 時速の変換公式】
- 「秒速 → 時速」 ○○(m / 秒)×3.6 = △△(km / 時)
秒速20mを時速△△kmに変換すると、
20(m / 秒)×3.6 = 72(km / 時)
- 「時速 → 秒速」 △△(km / 時)÷3.6 = ○○(m / 秒)
時速90kmを秒速○○mに変換すると、
90(km / 時)÷3.6 = 25(m / 秒)
更に時間を短縮したい方は、よく出題される秒速、時速の関係を覚えておきましょう。
| 秒速(m) | 時速(km) |
| 秒速15m | 時速54km |
| 秒速20m | 時速72km |
| 秒速25m | 時速90km |
| 秒速30m | 時速108km |
| 秒速35m | 時速126km |
| 秒速40m | 時速144km |
![]()
<基本問題>
長さ240mの列車が、時速108kmで電柱を通過する。 列車の最前部が電柱を通過し始めてから、最後部が通過し終えるまで何秒かかるか。 ただし、電柱の太さは考えないものとする。
列車の最前部に「旗」を立て、旗がどれだけ移動したかに注目する。
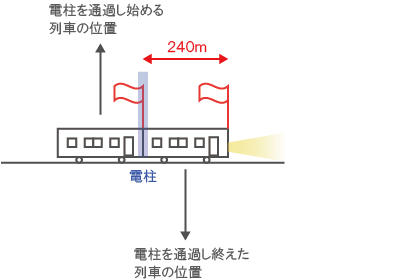
上図の通り、列車の最前部が電柱を通過し始めてから、最後部が通過し終えるまで、列車は240m進む。
秒数を求める問題なので、「△△(km / 時)÷3.6 = ○○(m / 秒)」を使って、時速を秒速に変換しておこう。
- 式)108÷3.6 = 30(m / 秒)
よって、かかる時間は、
- 式)[ 時間 ] = [ 距離 ]÷[ 速さ ]
= 240÷30
= 8(秒)
長さ200mの列車が、800mのトンネルに入り始めてから完全に出終えるまでに、50秒かかった。この列車の速さは時速何kmか。
A→D.時速72km
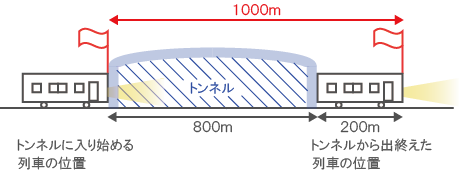
上図の通り、トンネルに入り始めてから完全に出終えるまでに、列車は1000m進む。
よって、列車の秒速は、
- 式)[ 速さ ] = [ 距離 ]÷[ 時間 ]
= 1000÷50
= 20(m / 秒)
求めるのは時速なので、「○○(m / 秒)×3.6 = △△(km / 時)」を使って、秒速を時速に変換する。
- 式)20×3.6 = 72(km / 時)
秒速20m、長さ150mの列車Aと、秒速15m、長さ200mの列車Bがすれ違った。 お互いの最前部がすれ違い始めてから、お互いの最後部がすれ違い終えるまでに何秒かかるか。
上図の通り、特急列車が問題の条件を満たすためには、各列車は合わせて350m離れる必要がある。
「旗がピタリと揃っている状態から、350m離れている状態になる」と考えると分かりやすい。
すれ違う速さは、各列車の速さの和になるので、
- 式)15 + 20 = 35(m / 秒)
よって、かかる時間は、
- 式)[ 時間 ] = [ 距離 ]÷[ 速さ ]
= 350÷35
= 10(秒)
長さ150mの列車が、時速72kmで長さ900mのトンネルを通過する。トンネルに完全に隠れているのは何秒か。
A→D37.5秒
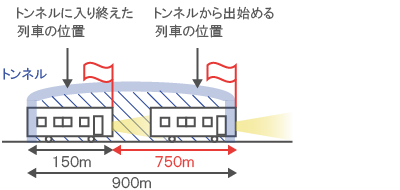
上図の通り、トンネルに完全に隠れている間、列車は750m進む。
秒数を求める問題なので、時速を秒速に変換しておこう。
- 式)72÷3.6 = 20(m / 秒)
よって、完全に隠れている時間は、
- 式)[ 時間 ] = [ 距離 ]÷[ 速さ ]
= 750÷20
= 37.5(秒)
時速108km、長さ200mの特急列車が、時速72km、長さ150mの急行列車を追い抜く。 特急列車の最前部が急行列車の最後部に追いつき始めてから、 特急列車の最後部が急行列車の最前部を追い抜き終えるまで何秒かかるか。
A→B 35秒
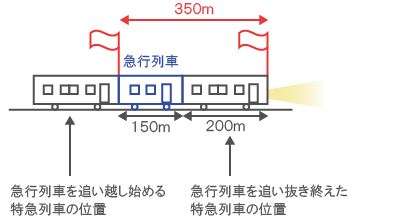
上図の通り、特急列車が問題の条件を満たすためには、急行列車と比べて350m先に進む必要がある。
特急列車が急行列車を追い抜く速さは、
- 式)108 – 72 = 36(km / 時)
これを秒速に変換すると、
- 式)36÷3.6 = 10(m / 秒)
よって、追い抜き終えるまでにかかる時間は、
- 式)[ 時間 ] = [ 距離 ]÷[ 速さ ]
= 350÷10
= 35(秒)
