<ポイント>
人や物の流れを数式で表す問題です。
中学や高校で勉強しない分野であること
数式に多くの記号が使われること
・・・などから難しそうな問題のように見えるのですが・・・(ノ∀`;)
しかし実は、ルートを列挙することで、誰でも簡単に解くことができます!
- 基本の図と数式を覚えておこう!
- スタート地点からゴール地点までのルートを全て列挙しよう!
【基本ルール】(どの問題でも最初に説明されます。)
下図は、X会場にいる人のうちpの割合がY会場に進むことを表している。
![]()
このとき、X会場にいる人を「X」、Y会場にいる人を「Y」とすると、「Y = pX」の数式が成り立つ。
下図は、X会場にいる人のうちpの割合がZ会場に進み、Y会場にいる人のうちqの割合がZ会場に進むことを表している。
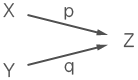
このとき、「Z = pX + qY」の数式が成り立つ。
下図は、X会場にいる人のうちpの割合がY会場に進み、さらにそのうちのqの割合がZ会場に進むことを表している。
![]()
このとき、「Z = qY」の数式が成り立つ。
また、「Z = q(pX) = pqX」とも表せる。
なお、これらの数式には次のような一般の演算が成り立つ。
(p + q)X = pX + qX
r(p + q)X = prX + qrX
「物の流れと比率」が出題される場合、上記のような「基本ルール」が示されます。
この基本ルールはどの問題でも変わらないので、あらかじめ覚えておきましょう。
![]()
<基本問題>
次の図は、W会場とX会場からZ会場に進んだ人を表したものである。
(基本ルールは省略します。)
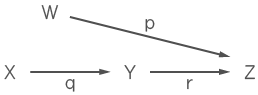
次のうち、正しい数式はどれか。
- アZ = pW + qrX
- イZ = pW + rY
- ウZ = pW + (q + r)X
スタート地点(W、X)からゴール地点(Z)までのルートを全て列挙する。
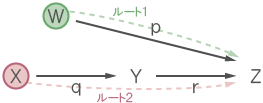
ルート1:pW
ルート2:qrX
これらのルートの和が「Z」を表す正しい数式である。
それでは、選択肢の数式を確認していこう。
アZ = pW + qrX → 正しい。
「pW + qrX」は、ルート1「pW」とルート2「qrX」の和となっている。
イZ = pW + rY → 正しい。
「rY = r(qX) = qrX」である。
よって、「pW + rY」は、ルート1「pW」とルート2「qrX」の和となっている。
ウZ = pW + (q + r)X → 正しくない。
「pW + (q + r)X」は、ルート1「pW」は正しく表しているが、ルート2を表す数式が誤っている。ルート2は「qrX」である。
よって、正しい数式はアとイの両方である。
次の図は、S会場とT会場とV会場とX会場からZ会場に進んだ人を表したものである。
(基本ルールは省略します。)
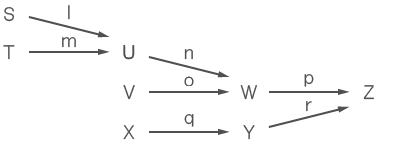
次のうち、正しい数式はどれか。
- アZ = lnpS + opV + qrX
- イZ = p(nU + oV) + rY
- ウZ = pW + (q + r)X
A→B.イだけ
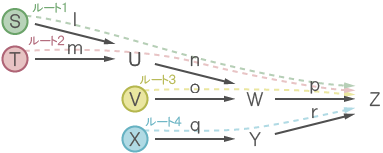
ルート1:lnpS
ルート2:mnpT
ルート3:opV
ルート4:qrX
これらのルートの和が「Z」を表す正しい数式である。
それでは、選択肢の数式を確認していこう。
アZ = lnpS + opV + qrX → 正しくない。
lnpS → ルート1
opV → ルート3
qrX → ルート4
よって、ルート2を表す数式がないため、正しくない。
イZ = pW + rY → 正しい。
pW = p(nU + oV)
= npU + opV
= np(lS + mT) + opV
= lnpS + mnpT + opV → ルート1 + ルート2 + ルート3
rY = r(qX) = qrX → ルート4
よって、全てのルートを正しく表している。
ウZ = pW + (q + r)X → 正しくない。
pW = p(nU + oV)
= npU + opV
= np(lS + mT) + opV
= lnpS + mnpT + opV → ルート1 + ルート2 + ルート3
(q + r)X → 誤り。ルート4は「qrX」
よって、ルート4を表す数式が誤っているため、正しくない。
したがって、正しい数式はイだけである。
なお、この解説では分かりやすさを重視しているため、イ、ウの数式を展開しているが、本試験ではこのような時間はない。
数式を展開しなくても、「全てのルートをもれなく表しているかどうか」を判断できるようにしておきたい。
