<ポイント>
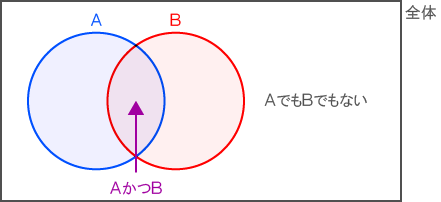
集合のイメージが持ちやすい![]() ベン図
ベン図
計算式が導きやすい![]() カルノー表
カルノー表
・・・ということで、念のため両方の解き方で解説します。
私はベン図でイメージをつかむのが好きですが、どうしても苦手な方はカルノー表を使って下さい~ヽ(o´∀`o)ノ
「ベン図」または「カルノー表」で、素早く情報を整理しよう!
[ ベン図 ]
| A○ | A× | 合計 | |
| B○ | XX | XX | XX |
| B× | XX | XX | XX |
| 合計 | XX | XX | XX |
![]()
<基本問題>
ある大学で100人の学生を対象に、通学時の電車とバスの利用状況についてアンケートを取った。 その結果、電車を利用している学生は70人、バスを利用している学生は35人いた。 また、電車とバスの両方を利用している学生は25人であった。 このとき、電車とバスを両方とも利用していない学生は何人か。
【ベン図】
下図の通り、ベン図に情報をまとめる。
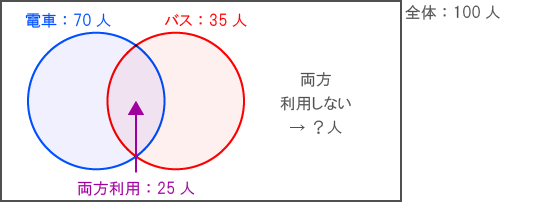
ベン図から計算式を導こう!
「青」(電車)と「赤」(バス)と「外」(両方利用しない)を足して・・・
「重なり」(両方利用)を引けば・・・
「全体」になることがイメージできる。
※ 「青」と「赤」を足した時点で「重なり」が2回足されてしまっているので引く(*´∀`*)
- 式)70 + 35 + X – 25 = 100
80 – X = 100
X = 20(人)
【カルノー表】
与えられた情報を表にまとめる。求めるのは、黄色マスである。
| バス○ | バス× | 合計 | |
| 電車○ | 25 | 70 | |
| 電車× | ? | 30 | |
| 合計 | 35 | 65 | 100 |
下表の通り、①→②の順で求めればよい。
- 式)① = 70 – 25 = 45(人)
- 式)② = 65 – 45 = 20(人)
| バス○ | バス× | 合計 | |
| 電車○ | 25 | ① 45 | 70 |
| 電車× | ② 20 | 30 | |
| 合計 | 35 | 65 | 100 |
表を書くのに少し時間がかかるが、簡単な引き算だけで解答できるため、ケアレスミスを減らせる。
![]()
Q1、文章で出題
大学生200人を対象に、飲酒と喫煙に関するアンケートを取った。 その結果、飲酒すると答えた学生は125人、喫煙すると答えた学生は65人いた。 また、飲酒も喫煙も両方しないと答えた学生は45人であった。 このとき、飲酒も喫煙も両方すると答えた学生は何人か。
【ベン図】
下図の通り、ベン図に情報をまとめる。

ベン図から計算式を導こう!
「青」(飲酒)と「赤」(喫煙)と「外」(両方しない)を足して・・・
「重なり」(両方する)を引けば・・・
「全体」になることがイメージできる。
※ 「青」と「赤」を足した時点で「重なり」が2回足されてしまっているので引く(*´∀`*)
- 式)125 + 65 + 45 – X = 200
235 – X = 200
X = 35(人)
【カルノー表】
与えられた情報をカルノー表にまとめる。求めるのは、黄色マスである。
| 喫煙○ | 喫煙× | 合計 | |
| 飲酒○ | ? | 125 | |
| 飲酒× | 45 | 75 | |
| 合計 | 65 | 135 | 200 |
下表の通り、①→②の順で求めればよい。
- 式)① = 75 – 45 = 30(人)
- 式)② = 65 – 30 = 35(人)
| 喫煙○ | 喫煙× | 合計 | |
| 飲酒○ | ② 35 | 125 | |
| 飲酒× | ① 30 | 45 | 75 |
| 合計 | 65 | 135 | 200 |
Q2、表で出題
150人を対象に、商品Pに関するアンケート調査を行った。下表は、調査項目と集計結果である。
| 調査項目 | 回答 | |
| 価格は満足ですか? | 満足している | 80人 |
| 満足していない | 70人 | |
| 品質は満足ですか? | 満足している | 110人 |
| 満足していない | 40人 | |
価格も質も両方満足している人が65人のとき、価格も質も両方満足していない人は何人いるか。
【ベン図】
問題1は文章で、問題2では表で情報が与えられているが、解き方は変わらない。
下図の通り、ベン図に情報をまとめる。
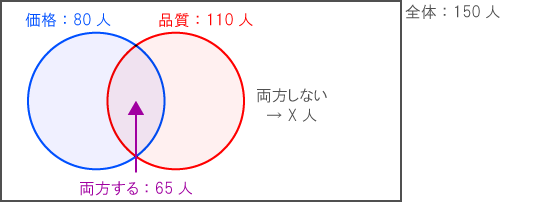
「青」と「赤」と「外」を足して・・・
「重なり」を引けば・・・
「全体」になることがイメージできる。
- 式)80 + 110 + X – 65 = 150
125 + X = 150
X = 25(人)
【カルノー表】
与えられた情報を表にまとめる。求めるのは、黄色マスである。
| 品質○ | 品質× | 合計 | |
| 価格○ | 65 | 80 | |
| 価格× | ? | 70 | |
| 合計 | 110 | 40 | 150 |
下表の通り、①→②の順で求めればよい。
- 式)① = 80 – 65 = 15(人)
- 式)② = 40 – 15 = 25(人)
| 品質○ | 品質× | 合計 | |
| 価格○ | 65 | ① 15 | 80 |
| 価格× | ② 25 | 70 | |
| 合計 | 110 | 40 | 150 |
Q3、表で出題2
中学生500人を対象に、スポーツに関するアンケート調査を行った。下表は、調査項目と集計結果である。
| 調査項目 | 回答 | |
| バスケットボールをしたことがありますか? | ある | 280人 |
| ない | 220人 | |
| バスケットボールが好きですか? | 好き | 350人 |
| 嫌い | 150人 | |
| バレーボールをしたことがありますか? | ある | 330人 |
| ない | 170人 | |
| バレーボールが好きですか? | 好き | 390人 |
| 嫌い | 110人 | |
(1)バスケットボールをしたことがあり、かつ嫌いだと答えた人は60人いた。このとき、バスケットボールをしたことがなく、かつ好きだと答えた人は何人いるか。
【ベン図】
下図の通り、ベン図に情報をまとめる。
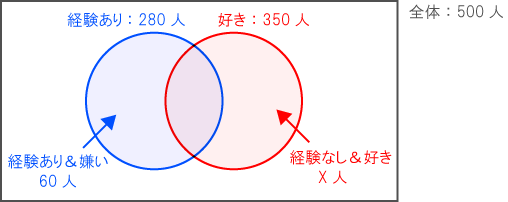
「青」と「赤」の「重なり」を求め・・・
その後「赤のみ」を求めよう!
- 式)280 – 60 = 220・・・「重なり」
- 式)350 – 220 = 130(人)・・・「赤のみ」
【カルノー表】
与えられた情報を表にまとめる。求めるのは、黄色マスである。
| 好き | 嫌い | 合計 | |
| 経験あり | 280 | ||
| 経験なし | ? | 220 | |
| 合計 | 350 | 150 | 500 |
下表の通り、①→②の順で求めればよい。
- 式)① = 150 – 60 = 90(人)
- 式)② = 220 – 90 = 130(人)
| 好き | 嫌い | 合計 | |
| 経験あり | 60 | 280 | |
| 経験なし | ② 130 | ① 90 | 220 |
| 合計 | 350 | 150 | 500 |
Q4、連立方程式
中学生500人を対象に、スポーツに関するアンケート調査を行った。下表は、調査項目と集計結果である。
| 調査項目 | 回答 | |
| バスケットボールをしたことがありますか? | ある | 280人 |
| ない | 220人 | |
| バスケットボールが好きですか? | 好き | 350人 |
| 嫌い | 150人 | |
| バレーボールをしたことがありますか? | ある | 330人 |
| ない | 170人 | |
| バレーボールが好きですか? | 好き | 390人 |
| 嫌い | 110人 | |
(2) バレーボールをしたことがなく、かつ好きだと答えた人は、バレーボールをしたことがあり、かつ嫌いだと答えた人の3倍いた。 このとき、バレーボールをしたことがなく、かつ嫌いだと答えた人は何人いるか。
【ベン図】
下図の通り、ベン図に情報をまとめる。
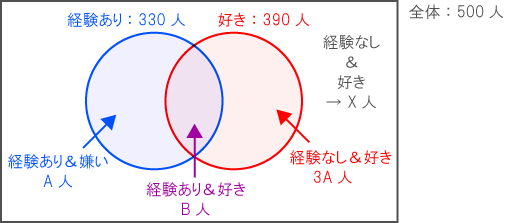
「青」と「赤」に注目して、連立方程式を立てる。

これで「重なり」が300人と分かる。
あとはいつも通り「青」と「赤」と「外」を足して・・・
「重なり」を引けば・・・
「全体」になるイメージで解ける。
- 式)330 + 390 + X – 300 = 500
420 + X = 150
X = 80(人)
【カルノー表】
与えられた情報を表にまとめる。求めるのは、黄色マスである。
「バレーボールをしたことがなく、かつ好きだと答えた人は、バレーボールをしたことがあり、かつ嫌いだと答えた人の3倍」なのだから バレーボールをしたことがあり、かつ嫌いだと答えた人の数を「A」と表すと、バレーボールをしたことがなく、かつ好きだと答えた人の数は「3A」と表せる。
また、バレーボールをしたことがなく、かつ嫌いだと答えた人の数は「B」としておこう。
| 好き | 嫌い | 合計 | |
| 経験あり | A | 330 | |
| 経験なし | 3A | B | 170 |
| 合計 | 390 | 110 | 500 |
表の「経験なし」の横軸の値から、方程式を立てると、3A + B = 170・・・①
表の「嫌い」の縦軸の値から、方程式を立てると、A + B = 110・・・②
① – ②より

したがって、バレーボールをしたことがなく、かつ嫌いだと答えた人は80人である。
Q5、表の関連
大学生の男性100人と女性100人を対象に、映画に関するアンケート調査を行った。下表は、調査項目と集計結果である。
| 調査項目 | 回答 | 男性 | 女性 |
| 俳優は良かったですか? | はい | 58人 | 70人 |
| いいえ | 42人 | 30人 | |
| ストーリーは良かったですか? | はい | 30人 | 24人 |
| いいえ | 70人 | 76人 |
俳優のみ良かったと回答した男性は40人、ストーリーのみ良かったと回答した女性は5人いた。
このとき、俳優もストーリーも両方良かったと回答した人は男女合わせて何人か。
【ベン図】
「価格と質の両方に満足していると回答した男性の数」と「価格と質の両方に満足していると回答した女性の数」をそれぞれ求めて、足し合わせればよい。
<男性を対象にしたベン図>
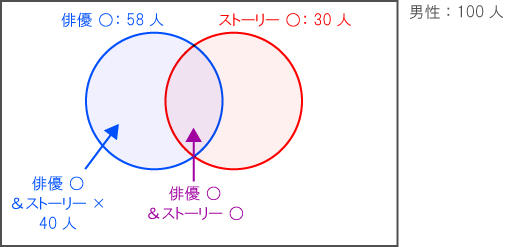
- 式)58 – 40 = 18(人)・・・「価格と質の両方に満足していると回答した男性の数」
<女性を対象にしたベン図>
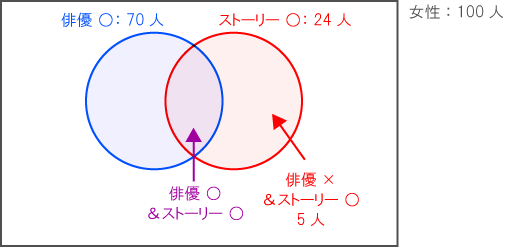
- 式)24 – 5 = 19(人)・・・「価格と質の両方に満足していると回答した女性の数」
- 式)18 + 19 = 37(人)・・・「男女の合計」
【カルノー表】
男性を対象にした表と、女性を対象にした表を描こう。
| ストーリー○ | ストーリー× | 合計 | |
| 俳優○ | ? | 40 | 58 |
| 俳優× | 42 | ||
| 合計 | 30 | 70 | 100 |
よって、価格と質の両方に満足していると回答した男性の数は
- 式)58 – 40 = 18(人)
| ストーリー○ | ストーリー× | 合計 | |
| 俳優○ | ? | 70 | |
| 俳優× | 5 | 30 | |
| 合計 | 24 | 76 | 100 |
よって、価格と質の両方に満足していると回答した女性の数は
- 式)24 – 5 = 19(人)
最後に、男女の数を合計する。
- 式)18 + 19 = 37(人)
Q6、最多、最少
100人を対象に、商品Pと商品Qに関するアンケート調査を行った。下表は、調査項目と集計結果である。
| 調査項目 | 回答 | |
| 商品Pは満足ですか? | はい | 63人 |
| いいえ | 37人 | |
| 商品Qは満足ですか? | はい | 88人 |
| いいえ | 12人 | |
このとき、商品Pも商品Qも両方満足していると回答した人は、最多で何人いるか。また、最少で何人いるか。
この問題はカルノー表を描いても分かりにくいので、ベン図を使って解く。
商品Pも商品Qも両方満足していると回答した人が最多になるのは、商品Qに満足している人の集合が、商品Pに満足している人の集合を完全に含んでいる場合である。
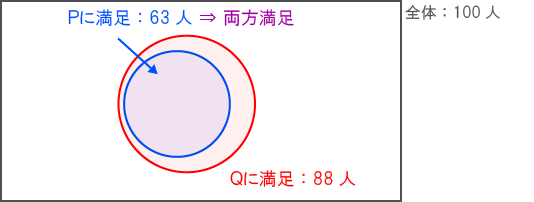
このとき、両方満足していると回答した人は63人である。
一方、商品Pも商品も両方満足していると回答した人が最少になるのは、 下図のように、両方満足ではない人が0人の場合である。

あとはいつも通り「青」と「赤」と「外を足して・・・
「重なり」を引けば・・・
「全体」になるイメージで解ける。
- 式)63 + 88 + 0 – X = 100
151 – X = 100
X = 51(人)
よって、最多で63人、最少で51人が答えとなる。
Q8、3集合
小学生180人に対し、野菜の好き嫌いについて、「好き」か「嫌い」かで答えるアンケートを行ったところ、ナスが好きな人は100人、ピーマンが好きな人は70人、ニンジンが好きな人は110人だった。このうち、ナスもピーマンも好きと答えた人は40人だった。また、ナス、ピーマン、ニンジン、いずれも嫌いと答えた人は1人もいなかった。
(1)ニンジンだけが好きな人は何人か。
集合が3つの問題は、カルノー図で表現しても分かりにくいので、ベン図で解く。
与えられた情報をベン図にまとめると、以下のようになる。
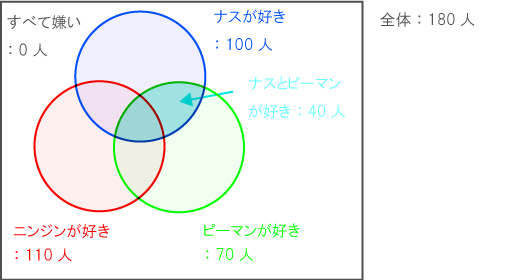
求めるのは以下の赤の領域。

上の水色の領域は以下によって求められる。

式)100 + 70 – 40 = 130(人)
よって、赤の領域は
式)180 -130 = 50(人)
Q9、3集合2
小学生180人に対し、野菜の好き嫌いについて、「好き」か「嫌い」かで答えるアンケートを行ったところ、ナスが好きな人は100人、ピーマンが好きな人は70人、ニンジンが好きな人は110人だった。このうち、ナスもピーマンも好きと答えた人は40人だった。また、ナス、ピーマン、ニンジン、いずれも嫌いと答えた人は1人もいなかった。
(2)ナスとニンジンが好きと答えた人は51人だった。また、ナスだけが好きと答えた人は、ナスが嫌いだが他の野菜はすべて好きと答えた人の4倍だった。このとき、すべての野菜が好きと答えた人は何人か。
与えられた情報をベン図にまとめると、以下のようになる。
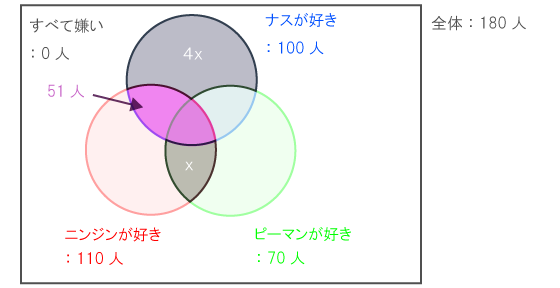
以下の図形は2通りの表現の仕方があるので、これらから方程式を立てる。
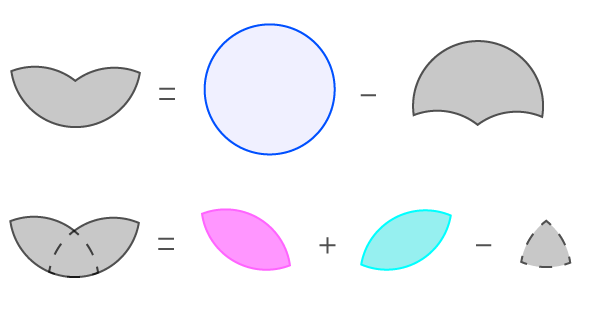
求める領域の人数をyとおくと、
式)100 – 4x = 51 + 40 – y
⇔ y = 4x – 9
(1)より、ニンジンだけが好きな人が50人なので、
式)x = 110 – 50 – 51 = 9(人)
したがって答えは、
式)4×9 – 9 = 27(人)
