速度算について

＜ポイント＞

「AとBが近寄ってゆく」「AがBを追いかける」のような状態を、正確にイメージできるかどうか。
○.○時間 → △△時間□□分の変換（例：2.1時間 = 2時間06分）などがポイントです！(*´∀｀*)

 

  • 基本の3公式を覚えておこう！（いや。やはり無理に覚えなくてもてもいい。理由は後述。）
  • どのくらいの距離をどのくらいの速さで進む（縮める）のかを正確に把握しよう！
  • 「時間」と「分」を正確に使い分けよう！

【公式】

  1. 公式① [ 距離 ] = [ 速さ ]×[ 時間 ]
  2. 公式② [ 速さ ] = [ 距離 ]÷[ 時間 ]
  3. 公式③ [ 時間 ] = [ 距離 ]÷[ 速さ ]

公式①を意識しなきゃ使えない人
時速30kmで2時間走ったら、何km進むのかなぁ？ハテナ？そうだ！公式に当てはめて・・・みたいな人
多分、SPI受ける人の中には一人もいないでしょうね・・・(ノ∀｀；)
なので、正直ページの無駄なんですが、どの参考書にもデカデカ載ってて「覚えろ！」みたいに書いてあるので、一応ね・・・。

【時間と分の変換方法】

「時間」→「分」

○.○時間を△△時間□□分に変換するためには、○.○の小数点以下を取り出して60倍します。
例として、2.15時間を△△時間□□分に変換してみましょう。0.15を取り出して、60倍するため、

  1. 式）0.15×60 = 9（分）

したがって、「2.15時間」は「2時間9分」と表せます。

「分」→「時間」

△△時間□□分を○.○時間に変換するためには、□□を取り出して1 / 60倍します。
例として、2時間24分を○.○時間に変換してみましょう。24を取り出して、1 / 60倍するため、

  1. 式）24×（1 / 60） = 2 / 5（時間） または 0.4（時間）

したがって、「2時間24分」は「2 + 2 / 5時間」または「2.4時間」と表せます。

 

 

＜基本問題＞

Lは時速5kmでP地点からQ地点に向かって、Mは時速7kmでQ地点からP地点に向かって、同時に歩き始めた。
P地点からQ地点までの距離が32kmであるとき、LとMが最初に出会うのは、LとMが出発してから何時間何分後か。

A1時間40分後
B2時間後
C2時間20分後
D2時間40分後
E3時間後
F3時間20分後
G3時間40分後
H4時間後

Ａ→２時間40分後

上図の通り、互いに近づいていくため、距離は1時間に12kmずつ縮まる。

  1. 式）5 + 7 = 12（km / 時）

したがって、出会うまでの時間は、

  1. 式）[ 時間 ] = [ 距離 ]÷[ 速さ ]
    = 32 / 12
    = 8 / 3
    = 2 + 2 / 3（時間後）

○○時間を△△分に変換するためには60倍すればよい。2 / 3時間を△△分に変換すると、

  1. 式）（2 / 3）×60 = 40（分）

2時間40分後が答えとなる。

 

 

下表は、P停留所を出発し、Q停留所を通ってR停留所に至るバスの時刻表である。

（1）PQ間の距離が15kmであるとき、PQ間の平均時速はいくらか。

  1. A50km / 時
  2. B52km / 時
  3. C54km / 時
  4. D56km / 時
  5. E58km / 時
  6. F60km / 時
  7. G62km / 時
  8. H64km / 時

（2）QR間の平均時速が54kmであるとき、QR間の距離は何kmか。

  1. A8.0km
  2. B8.4km
  3. C8.8km
  4. D9.2km
  5. E9.6km
  6. F10.0km
  7. G10.4km
  8. H10.8km
　Ａ→（1）50km / 時

PQ間の所要時間は18分である。
よって、バスの平均時速は、

  1. 式）[ 速さ ] = [ 距離 ]÷[ 時間 ]
    = 15÷（18 / 60）
    = 15÷（3 / 10）
    = 15×（10 / 3）
    = 50（km / 時）

求めたいのは「分速」ではなく「時速」なので、「18分」を「18 / 60時間」に変換してから計算することに注意しよう。

Ａ→（2）　H．10.8km

QR間の所要時間は12分である。

よって、QR間の距離は、

  1. 式）[ 距離 ] = [ 速さ ]×[ 時間 ]
    = 54×（12 / 60）
    = 54×（1 / 5）
    = 10.8（km）

問題文のバスの速度は「分速」ではなく「時速」で表されているため、「12分」を「12 / 60時間」に変換してから計算することに注意しよう。

 

 

Ｑ1、コースを回る

PとQの2人は、1周24kmのマラソンコースを走る。 Pは時速12km、Qは時速18kmで走り、2人の速度はそれぞれ常に一定であるものとする。

（1）今、2人はマラソンコース上の同じ地点にいる。PとQが反対方向に同時に走り出すとき、2人が再び出会うのは何分後か。

Ａ→48分後

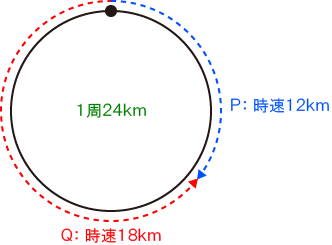
  • 再び出会うまで、2人はマラソンコース1周分の24kmを走る。
    上図の通り、互いに近づいていくため、距離は毎時30km（12 + 18）ずつ縮まる。
  • よって、出会う時間は、
  1. 式）[ 時間 ] = [ 距離 ]÷[ 速さ ]
    = 24 / 30
    = 4 / 5（時間後）
  • ○○時間を△△分に変換するためには60倍すればよい。4 / 5時間を△△分に変換すると、
  1. 式）（4 / 5）×60 = 48（分後）
  • 48分後が答えとなる。

 

 

Ｑ2．コースを回る2

PとQの2人は、1周24kmのマラソンコースを走る。 Pは時速12km、Qは時速18kmで走り、2人の速度はそれぞれ常に一定であるものとする。

（2）今、2人はマラソンコース上の同じ地点にいる。Qが走り始めてから50分後にPが同じ方向に走り始めるとき、Qが最初にPに追いつくのはPが走り始めてから何時間何分後か。

 

Ａ→時間30分後
  • まず、Pが走り始める時のQの地点を調べる。
    Qが50分で走る距離は、
  • 式）[ 距離 ] = [ 速さ ]×[ 時間 ]
    = 18×（50 / 60）
    = 15（km）
  • よって、Qはスタート地点の9km手前にいる。

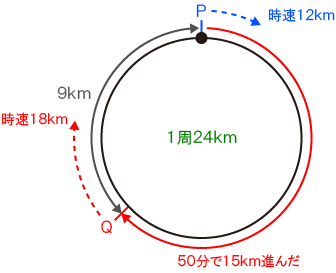
  • Pが走り始めた後、時速18kmのQが、時速12kmのPを追う形となる。
    9kmの差は毎時6km（18 – 12）ずつ縮まる。
    したがって、Qが最初にPに追いつくのは、
  • 式）[ 時間 ] = [ 距離 ]÷[ 速さ ]
    = 9 / 6
    = 3 / 2
    = 1 + 1 / 2（時間後）
  • 1時間30分後が答えとなる。

 

 

Ｑ3、時刻表

下表は、Lが徒歩でP地点を出発し、Q地点を経由してR地点に至るまでの発着時刻である。

「速度算」問題2 図1 Copyright （C） - SPI無料学習サイト（SPI3対応）【Study Pro】
  • （1）LがPQ間を時速5.1kmの等速度で歩いているとき、PQ間の距離は何kmか。
  • A→3.4km
  • PQ間の所要時間は40分である。
    よって、PQ間の距離は、
  • 式）[ 距離 ] = [ 速さ ]×[ 時間 ]
    = 5.1×（40 / 60）
    = 3.4（km）

 

 

Ｑ4、時刻表2

下表は、Lが徒歩でP地点を出発し、Q地点を経由してR地点に至るまでの発着時刻である。

「速度算」問題2 図1 Copyright （C） - SPI無料学習サイト（SPI3対応）【Study Pro】

（2）QR間を、Lは時速4.8kmの等速度で歩き、Mは時速12.8kmの等速度で走る。LがQ地点を出発した40分後に、MがQ地点を出発して追いかけると、MがLに追いつくのは何時何分か。

 

Ａ→11時39分
  • まず、MがQ地点を出発するとき、Lがどの地点にいるのかを調べる。
    Lが40分で歩く距離は、
  • 式）4.8×（40 / 60） = 3.2（km）
  • よって、Lは下図のように3.2km先行している。
「速度算」問題2 図2 Copyright （C） - SPI無料学習サイト（SPI3対応）【Study Pro】
  • MがQ地点を出発した後、時速12.8kmで走るMが、時速4.8kmで歩くLを追う形となる。
    3.2kmの差は毎時8kmずつ縮まる。
    したがって、MがLに追いつくのは、
  • 式）3.2÷8 = 0.4（時間後）
  • ○○時間を△△分に変換するためには60倍すればよい。0.4時間を分に変換すると、
  • 式）0.4×60 = 24（分後）
  • よって、MがLに追いつくのは、Mが出発してから24分後である。
    Mが出発するのは、Lが出発した40分後の11時15分なので、追いつくのは11時39分である。

 

 

Ｑ５、方程式

LがP地点とQ地点を往復したところ、4時間24分かかった。 行きは時速6km、帰りは時速5kmで歩いたとすると、P地点からQ地点までの距離は何kmか。

Ａ→12km
  • 「4時間24分」という形のまま計算するのは難しいので、「○.○時間」の形に変換しておこう。
    △△時間□□分を○.○時間に変換するためには、□□を取り出して1 / 60倍すればよい。
  • 式）24×（1 / 60） = 0.4（時間）
  • よって、「4時間24分」は「4.4時間」と表せる。
  • P地点からQ地点までの距離を「A」とすると、行きの所要時間は「A / 6」、帰りの所要時間は「A / 5」と表せる。
    よって、「行きの所要時間 + 帰りの所要時間 = 往復の所要時間」より、以下の方程式が成り立つ。
  • 式）A / 6 + A / 5 = 4.4
    （5A + 6A） / 30 = 4.4
    11A = 4.4×30
    A = 4.4×30÷11
    A = 12（km）
  • したがって、12kmが答えとなる。

 

 

Ｑ6、時刻表3

下表は、P駅を出発し、Q駅、R駅、S駅を通ってT駅に至る電車の時刻表である。

「速度算」問題2 図1 Copyright （C） - SPI無料学習サイト（SPI3対応）【Study Pro】

（1）PQ間の平均時速が108km、PR間の距離が98kmであるとき、QR間の平均時速はいくらか。

 

Ａ→124km / 時
  • まず、PQ間の距離を求める。
  • 式）[ 距離 ] = [ 速さ ]×[ 時間 ]
    = 108×（20 / 60）
    = 36（km）
  • よって、QR間の距離は、
  • 式）98 – 36 = 62（km）
  • したがって、QR間の平均時速は、
  • 式）[ 速さ ] = [ 距離 ]÷[ 時間 ]
    = 62÷（30 / 60）
    = 62÷（1 / 2）
    = 62×（2 / 1）
    = 124（km / 時）

 

 

Ｑ7、時刻表4

下表は、P駅を出発し、Q駅、R駅、S駅を通ってT駅に至る電車の時刻表である。

「速度算」問題2 図1 Copyright （C） - SPI無料学習サイト（SPI3対応）【Study Pro】

（2）RS間の平均時速が110km、ST間の平均時速が130km、RT間の距離が187kmであるとき、S駅を通過したのは何時何分か。

 

Ａ→11時24分
  • RT間の所要時間は1時間30分、つまり1.5時間なので、RS間の所要時間を「A」時間とすると、ST間の所要時間は「1.5 – A」時間と表せる。
    よって、「RS間の距離 + ST間の距離 = RT間の距離」より、以下の方程式が成り立つ。
  • 式）110×A + 130×（1.5 – A） = 187
    110A – 130A + 195 = 187
    -20A = -8
    20A = 8
    A = 0.4（時間）
  • したがって、RS間の所要時間は0.4時間である。
    0.4時間は24分（0.4×60）なので、S駅を通過したのは11時24分となる。

 

 

 

Ｑ8、予定より遅れる

Xは人との待ち合わせでP町まで自転車で行くことになった。予定時刻に着くために平均時速10kmで向かえば良いように家を出たが、家を出てすぐに忘れ物に気づき、予定より5分遅れて出発した。遅れた分を取り戻そうと、平均時速12kmで向かったところ、予定時刻丁度にP町に到着した。予定では家からP町まで何分かかるはずだったか。

 

Ａ→30分
  • 時間の比と速さの比を比較するのが一番速い！
    小難しい「分 ⇔ 時間」の計算をすっ飛ばして解答まで一直線(*´∀｀*)
  • [比]
  • かかるはずだった時間をx分とおけば、実際にかかった時間は（x – 5）分。
  • 走る距離は一定で、速さの比が10 : 12 = 5 : 6なので、かかった時間の比は6 : 5。
    x :（x – 5）= 6 : 5
  • 以上より、5x = 6（x – 5）
  • これを解くと、x = 30（分）
  • [比を使わない方法（力技）]
  • 比を使わない場合、
    ① 予定通りの場合と実際の場合を比較した方程式を立てて、P町までの距離を求めてから
    ② 予定通りなら何分かかったか計算する
    という手順を踏む必要がある。
  • P町までの距離をxkmとすると、予定通りの場合にかかる時間は、（x / 10）時間。
    実際にかかった時間は（x / 12）時間。
  • 5分遅れたことを考えて方程式を立てると、
    （x / 10） = （x / 12）+ （5 / 60）
    ※単位は時間。
  • 両辺に60をかけると、
    6x = 5x + 5
  • よって、x = 5（km）
  • これを予定通りの速さ、時速10kmで割ると、
  • 式）5÷10 = 0.5（時間）= 30（分）