<ポイント>
- 順列と組合せの公式は確実に!・・・例題1、例題2
- 「少なくとも・・・」ときたら「問題文と反対の条件の場合の数」を考え、全体の総数から引こう!・・・例題3
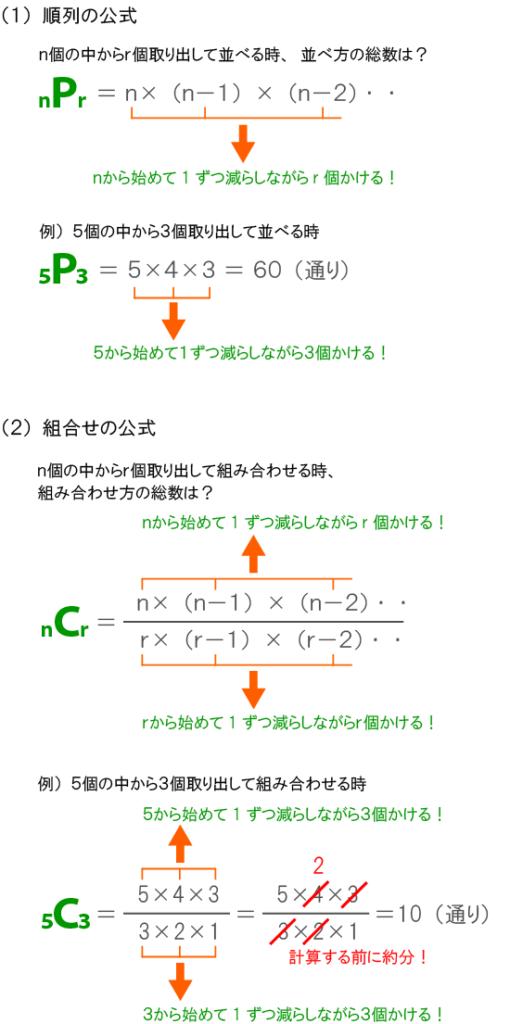
円順列の問題・・・問題4
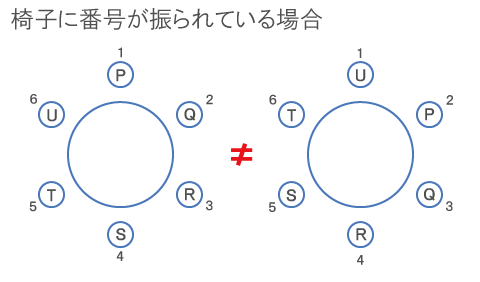
椅子に番号が振られているかどうかで状況が違う!
番号が振られていない場合は、相対的な位置関係が合致するものは「同配置」と見なされる。
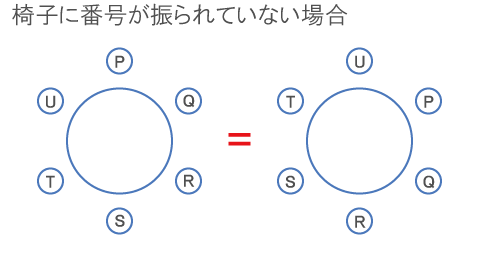
![]()
<基本問題>
- 1、2、3、4の数字が書かれた4枚のカードがある。この4枚から3枚を並べて3桁の整数を作るとき、何通りの作り方があるか。
- A→24通り
- 「順列」の理解を深めるために、1ステップずつ丁寧に解説する。
場合の数が得意な人はここはスキップ。
こちらへどうぞ。 問題1-1(組み合わせ)
問題1-1(組み合わせ) - ① 4枚のカードから1枚を取り出して、1桁の整数を作ることを考えると、この作り方は4通りある。
- ② 4枚のカードから2枚を取り出して、2桁の整数を作ることを考えると、下図のようになる。
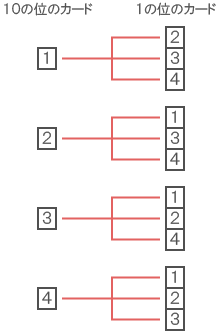
- まず、10の位を考えると、4通りのカードが考えられる。
次に、各々の10の位に対する1の位を考えると、10の位に1枚カードを使っているので、3通りのカードが考えられる。
よって、2桁の整数の作り方の数は - 式)4×3 = 12(通り)
- ③ 4枚のカードから3枚を取り出して、3桁の整数を作るときも、同様に考えればよい。
- 式)4×3×2 = 24(通り)
- この考え方が「順列」である。
問題文を順列の公式に当てはめると、同様に24通りと答えが出る。
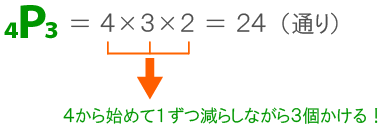
![]()
Q1、組み合わせ
あるサークルには、男性6人と女性4人が所属している。この中から掃除当番を4人選びたい。
(1)男性だけから4人選ぶとすると、選び方は何通りあるか。
組合せの公式を使い、6人から4人を選ぶ組合せの数を求める。
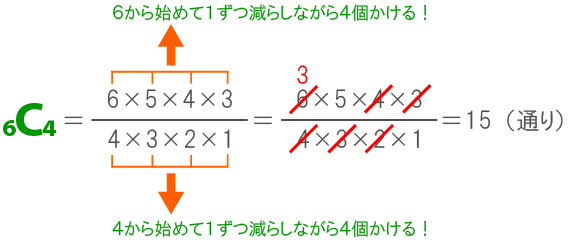
(場合の数が苦手な方は、こちらで公式を確認して下さい。)
Q2,組み合わせ2
あるサークルには、男性6人と女性4人が所属している。この中から掃除当番を4人選びたい。
(2)男性から2人、女性から2人選ぶとすると、選び方は何通りあるか。
- 男性6人から2人を選ぶ組合せの数は
- 式)6C2 = (6×5) / (2×1) = 15(通り)
- 女性4人から2人を選ぶ組合せの数は
- 式)4C2 = (4×3) / (2×1) = 6(通り)
- それぞれの組合せの数を掛け合わせる。
- 式)15×6 = 90(通り)
- 「それぞれの組合せの数を掛け合わせる」という考え方は、樹形図を想像すると分かりやすい。
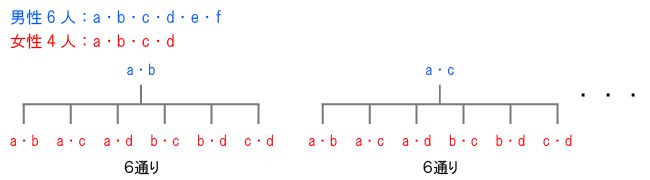
「a・b」「a・c」など、それぞれの男性の組合せに対して、6通りの女性の組合せが存在する。
これは他の全ての男性の組合せにも言えるので、組合せの数を掛け合わせれば、総数を求めることができる。
Q3,(少なくとも・・・)<余事象>
男性4人、女性5人で構成されるチームがある。この中から代表選手の3人を選びたい。
(1)男性が少なくとも1人は含まれるように選ぶとすると、その選び方は何通りか。
A→74通り
『少なくとも・・・』ときたら「問題文と反対の条件の場合の数」を考え、全体の総数から引く。
問題の条件である「男性が少なくとも1人は含まれる」の反対は、「男性が1人も含まれない」言い換えると「女性だけから選ぶ」である。
女性だけから選ぶ選び方の数は
- 式)5C3 = (5×4×3) / (3×2×1) = 10(通り)
- 一方、全体の総数は
- 式)9C3 = (9×8×7) / (3×2×1) = 84(通り)
- したがって、男性が少なくとも1人は含まれる選び方の数は
- 式)[ 全体の総数 ] – [ 女子だけから選ぶ選び方の数 ]
= 84 – 10
= 74(通り)
Q4、(少なくとも・・・)<余事象>
男性4人、女性5人で構成されるチームがある。この中から代表選手の3人を選びたい。
(2)男性と女性がそれぞれ少なくとも1人は含まれるように選ぶとすると、その選び方は何通りか。
問題の条件である「男性と女性がそれぞれ少なくとも1人は含まれる」の反対は、「女性だけから選ぶ」または「男性だけから選ぶ」である。
女性だけから選ぶ選び方の数は
- 式)5C3 = (5×4×3) / (3×2×1) = 10(通り)
- 男性だけから選ぶ選び方の数は
- 式)4C3 = (4×3×2) / (3×2×1) = 4(通り)
- 一方、全体の総数は
- 式)9C3 = (9×8×7) / (3×2×1) = 84(通り)
- したがって、男性と女性がそれぞれ少なくとも1人は含まれる選び方の数は
- 式)[ 全体の総数 ] – [ 女子だけから選ぶ選び方の数 ] – [ 男性だけから選ぶ選び方の数 ]
= 84 – 10 – 4
= 70(通り)
[ 別解 ]
- 男性と女性がそれぞれ少なくとも1人は含まれる選び方は、「男性2人 + 女性1人」の場合と「男性1人 + 女性2人」の場合が考えられるので、 それぞれの場合の数を求めて足し合わせてもよい。
- 男性2人と女性1人で選ぶ選び方の数は
- 式)4C2×5C1 = {(4×3) / (2×1)}×(5 / 1) = 30(通り)
- 男性1人と女性2人で選ぶ選び方の数は
- 式)4C1×5C2 = (4 / 1)×{(5×4) / (2×1)} = 40(通り)
- それぞれの場合の数を足し合わせる。
- 式)30 + 40 = 70(通り)
Q5,順列
P、Q、R、S、Tの5人を1列に並べる。
(1)Pを先頭に並べるとすると、その並び方は何通りか。
「Pを先頭に並べる」という条件があるので、Pを先頭に固定して、残りの4人の並び順が何通りあるかを考えればよい。
順列の公式を使おう。
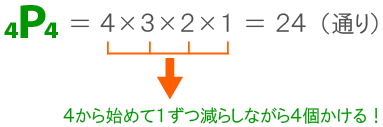
Q6、順列2
P、Q、R、S、Tの5人を1列に並べる。
(2)QとRの2人を続けて並べるとすると、その並び方は何通りか。
「QとRの2人を続けて並べる」という条件があるので、
まずQとRの2人を1つのグループにまとめ、「1つのグループ」と「他の3人」の計4つの並び順が何通りあるかを考える。
- 式)4P4 = 4×3×2×1 = 24(通り)
- QとRの並び順については、「Q→R」と「R→Q」の2パターンがあるため、これを2倍する。
- 式)24×2 = 48(通り)
Q7、円順列
P、Q、R、S、T、Uの6人が円形のテーブルのまわりに座らせる。
(1)P、Qが隣り合わせになるような座り方は何通りか。
円テーブルの場合の数の問題は、席に番号が振られているかどうかが大切!
番号が振られていない場合、相対的な位置関係が同じ配置は、全く同じものと見なされる。
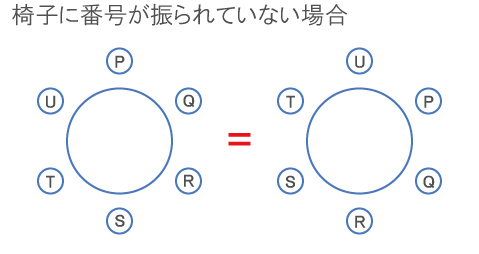
以下のように、P、Qを先頭に固定した列で考えても良い。
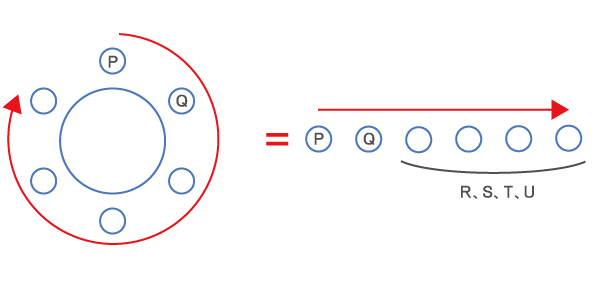
P、Qの場所の入れ替えで2通り、残りの4人の座り方の場合の数が4P4なので、
式)2×4P4 = 48 (通り)
なお、以下のパターンは全て同じものと見なされるので注意。
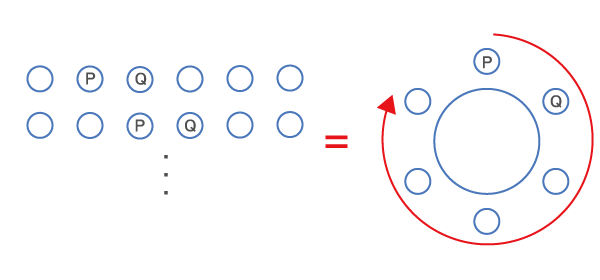
Q8、円順列2
P、Q、R、S、T、Uの6人が円形のテーブルのまわりに座らせる。
(2)PとQが隣りにならず、RとSが向かい合うような座り方は何通りか。
A→16通り
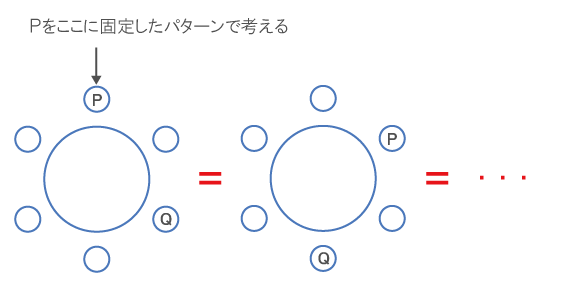
(1) 同様、回転させたら位置関係が同じになる場合を除きたいので、Pを固定して考える。
PとQの位置関係は以下の3パターンが考えられる。
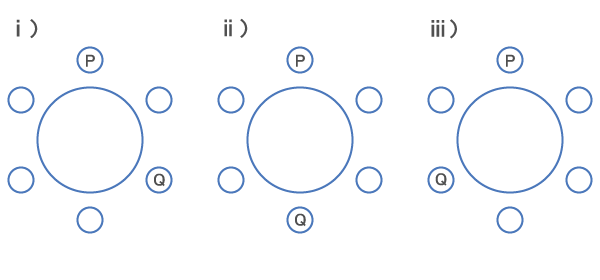
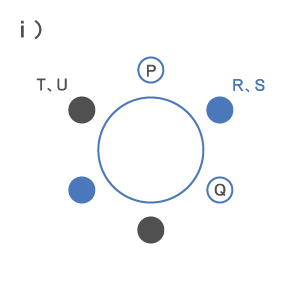
ⅰ)の場合、RとSが向かい合う席の組み合わせは1パターンしかない。
RとSの座り方が2通り、 残りの2人の座り方が2通りなので、
式)2×2 = 4(通り)
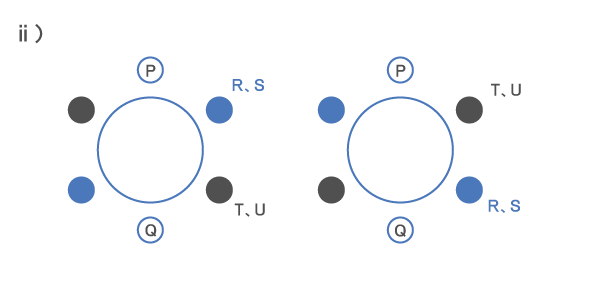
ⅱ)の場合、RとSが向かい合う席の組み合わせは2パターンある。
よって、RとSの座り方が2×2通り、 残りの2人の座り方が2通りなので、
式)4×2 = 8(通り)
ⅲ)はⅰ)と同じで4通り。
ⅰ)~ⅲ)を足し合わせると、
式)4 + 8 + 4 = 16(通り)
Q9、同じ物を何回使ってOK
0、1、2、3、4の5つの数字を使って、3桁の整数を作る。 同じ数字を何度使ってもよいが、百の位に0を使うことはできない。
(1)偶数は何通り作れるか。
- まず、各位の取り得る値を考える。
- 百の位 → 0を使えない → 1・2・3・4の4パターン
十の位 → 制限が無し → 0・1・2・3・4の5パターン
一の位 → 偶数 → は0・2・4の3パターン - 同じ数字を何度使ってもよいので、それぞれの数を掛け合わせる。
- 式)4×5×3 = 60(通り)
Q10、同じ物を何回使ってOK
0、1、2、3、4の5つの数字を使って、3桁の整数を作る。 同じ数字を何度使ってもよいが、百の位に0を使うことはできない。
(2)230より小さい数は何通り作れるか。
- 230より小さい数には、次の4パターンが考えられる。
- ① [百の位,十の位,一の位] = [2,2,□]
(一の位は、0・1・2・3・4のどれでもよい。) - ② [百の位,十の位,一の位] = [2,1,□]
(一の位は、0・1・2・3・4のどれでもよい。) - ③ [百の位,十の位,一の位] = [2,0,□]
(一の位は、0・1・2・3・4のどれでもよい。) - ④ [百の位,十の位,一の位] = [1,□,□]
(十の位と一の位は、0・1・2・3・4のどれでもよい。) - ①~③については、一の位はどれでもよいので、5通りの場合の数が考えられる。
④については、十の位と一の位はどれでもよいので、25通り(5×5)の場合の数が考えられる。 - したがって、求める場合の数は
- 式)5×3 + 25 = 40(通り)
Q11,コインの裏表
コインを6回連続で投げる。このとき、表が4回出るような表裏の出方は何通りか。
問題のコインの表裏を、白黒の碁石に置き換えて考える。
コインの表を白い碁石、コインの裏を黒い碁石に置き換えると、表が4回出るような表裏の出方は以下のように表せる。
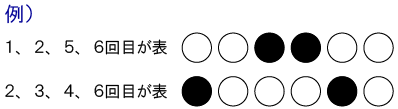
よって、碁石を配置する6個のスペースに、4個の白い碁石を配置する組合せの数を考えればよい。
- 式)6C4 = (6×5×4×3) / (4×3×2×1) = 15(通り)
Q12、配り方
青玉が1個、黄玉が2個、赤玉が2個ある。 これらをP、Q、R、S、Tの5人に1個ずつ配るとき、その配り方は何通りか。
- 青玉1個の配り方は、P、Q、R、S、Tの5通り。
- 黄玉2個の配り方は、残った4人の中から配る2人を選ぶので6通り。
- 式)4C2 = (4×3) / (2×1) = 6(通り)
- 赤玉2個の配り方は、残った2人に配ると決まっているので1通り。
- したがって、求める場合の数は
- 式)5×6×1 = 30(通り)
Q13、図形の塗分け
青、赤、黄、緑の4色からいくつかの色を使って、下図のA、B、C、Dを塗り分ける。このとき、同じ色を何回使ってもよいが、隣り合う部分の色が異なるような塗り方は何通りか。
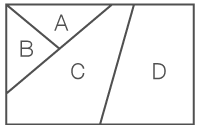
- 場合分けが必要となる問題。
- (1)すべての色が異なる場合 → 24通り
- 式)4P4 = 4×3×2×1 = 24(通り)
- (2)1つの色が2回使われる場合 → 48通り
- 隣り合う部分が異なる色であればよいため、AとDが同じ色、またはBとDが同じ色というパターンがある。
- 4色中3色で、[ (AとD)、B、C ]を塗り分ける場合の数は
- 式)4P3 = 4×3×2 = 24(通り)
- 同様に、[ (BとD)、A、C ]を塗り分ける場合の数も、24通りである。
- (1)と(2)以外の場合分けは条件を満たさない。
- 求める場合の数は
- 式)24 + 48 = 72(通り)
Q14、図形の塗分け2
赤、青、黄、緑、紫、黒の6色からいくつかの色を使って、下図のA、B、C、D、Eを塗り分ける。このとき、同じ色を何回使ってもよいが、隣り合う部分の色が異なるような塗り方は何通りか。
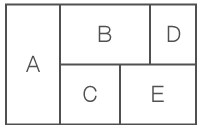
- (1)すべての色が異なる場合 → 720通り
- 式)6P5 = 6×5×4×3×2 = 720通り
- (2)1つの色が2回使われる場合 → 1080通り
- 隣り合う部分が異なる色であればよいため、AとDが同じ色、AとEが同じ色、CとDが同じ色という、3パターンがある。
- 6色中4色で塗り分ける場合の数は
- 式)6P4 = 6×5×4×3 = 360(通り)
- 3パターンがあるため
- 式)360×3 = 1080(通り)
- (3)2つの色が2回使われる場合 → 120通り
- AとEが同じ色で、CとDも同じ色というパターンがある。
- 6色中3色で塗り分ける場合の数は
- 式)6P3 = 6×5×4 = 120(通り)
- (1)、(2)、(3)以外の場合分けは条件を満たさない。
- 求める場合の数は
- 式)720 + 1080 + 120 = 1920(通り)
