<ポイント>
【N進法の基本】
N進法が出題される場合は下記の対応表が示されます。
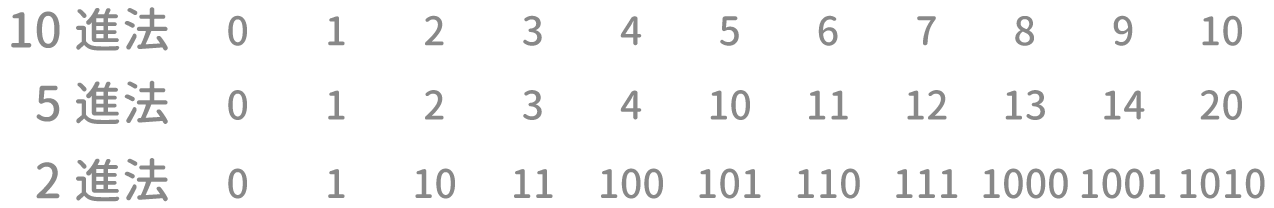
N進法の問題の基本形式は「○進法の△△△は、□進法ではどう表されるか。」といったものです。
しかし、△△△の数字があまりに大きいので、この対応表は問題を解く手掛かりにはなりません。
(2進法や5進法がどのようなものかを説明するだけの対応表です。)
そのため、問題を解くためには、事前に下記の最速解法を覚えておく必要があります。
(1) N進法で表現された数を10進法に変換する。・・・例題1
N進法で表現された数を10進法に変換するためには、下記の公式を使います。
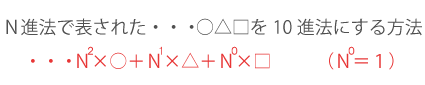
例えば、4進法の123を、10進法に変換すると次のようになります。
- 式)42×1 + 41×2 + 40×3 = 27
(2)10進法で表現された数をN進法に変換する。・・・例題2
10進法で表現された数をN進法に変換するためには元の数を、変換するN進法のNで割っていき、余りと最後の商を逆順に並べます。
例えば、10進法の58を3進法に変換すると次のようになります。
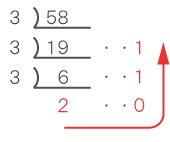
したがって、10進法の58を3進法に変換すると、2011である。
(3) N進法で表現された数を、別のN進法に変換する。
(1) → (2)を順番に実施すると、変換することができます。
(ここまでのことを覚えておけば、SPI試験のN進法の問題は解くことができます。興味のある方は下記の補足説明をご覧ください。)
【補足説明】
N進法に対する理解を深める前に、 私たちが日常生活で使っている10進法について考えてみましょう。
下図は、10進法の仕組みを図に表したものです。
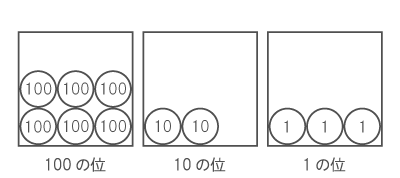
10進法がそう呼ばれるゆえんは、上図に例えて言うと、 「各箱の中に入っている○が10個になると、その箱の中身は空になり、代わりに左の位の箱の○が1つ増えることになる」という仕組みにあります。
したがって、一番右の箱に入っている○は1の重みしかありませんが、 真ん中の箱に入っている○1つは、一番右の箱の○ 10個分の重みがあり、一番左の箱に入っている○1つは、一番右の箱の○ 100個分の重みがあります。
そのため、これら全ての箱に入っている○の量を測ると
- 式)1×3 + 10×2 + 100×6 = 623
となります。
前置きが長くなりましたが、他のN進法も同様に考えてみましょう。
ここでは、4進法を例に挙げます。
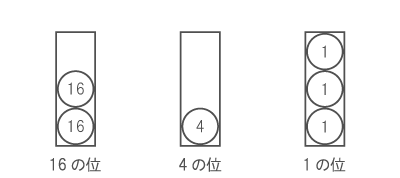
4進法がそう呼ばれるゆえんは、上図に例えて言うと、 「各箱の中に入っている○が4個になると、その箱の中身は空になり、代わりに左の位の箱の○が1つ増えることになる」という仕組みにあります。
したがって、一番右の箱に入っている○は1の重みしかありませんが、 真ん中の箱に入っている○1つは、一番右の箱の○ 4個分の重みがあり、一番左の箱に入っている○1つは、一番右の箱の○ 16個分の重みがあります。
そのため、これら全ての箱に入っている○の量を測ると
- 式)16×2 + 4×1 + 1×3 = 39
となります。
これは、「39個の○がある」という意味であり、自然と4進法を10進法に変換したことになります。
私たちは10進法に慣れているため変換したことに気づきにくいですが、「39個の○がある」と認識したときに使っている規則が10進法なのです。
以上のことから、N進法で表現された数を10進法に変換するためには、下記の公式を使えばよいと分かります。
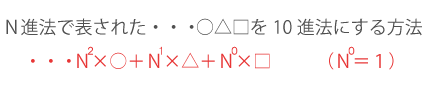
![]()
<基本問題>
3進法の2120は10進法ではどのように表現されるか。
- A69
- B70
- C71
- D72
- E73
- F74
- G75
- H76
- 式)33×2 + 32×1 + 31×2 + 30×0 = 69
10進法の155を4進法ではどのように表現されるか。
- A2113
- B2120
- C2121
- D2122
- E2123
- F2130
- G2131
- H2132
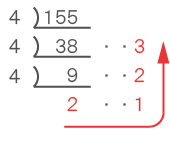
- 式)62×3 + 61×4 + 60×5 = 137
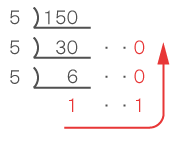
10進法で表現された150を、変換後の5進法の5で割っていき、余りと最後の商を逆順に並べる。
答えは、1100となる。
(10進法→N進法の最速解法については、例題をご覧下さい。)
SPI試験で見直しの余裕を持てることは少ないが、この問題はミスが多いため、時間が余ったときは是非確認してほしい。
確認は、N進法を再び10進法に戻すことで行う。
今回は、5進法で表された1100を10進法で表す。
- 式)53×1 + 52×1 + 51×0 + 50×0 = 150
このように、問題文の10進法と一致すれば、回答が正しいことを確認できる。
