<ポイント>
食塩水の濃度、食塩の量、水の量などを求める問題。
方程式、連立方程式を立てれば誰でも解くことができますが、
当サイトでは対SPIの公式や、面積図を使った方法も紹介します!(*´∀`*)
(1) 一種類の食塩水の食塩と水の内訳を問う問題・・・例題1
食塩水の構造をイメージすると、自然と式が導けます。
(2) 2つの食塩水に関する問題・・・例題2
下記の公式を利用します。
- 公式① [食塩水(g)]×[濃度(小数)] = 食塩(g)
- 公式② [食塩水(g)/ 100]×[濃度(整数)] = 食塩(g)・・・(食塩水の量がx00gのときに利用)
食塩水の量がx00gのときは、公式①ではなく、 公式②を利用すると計算が楽になります。
例えば、8%の食塩水300gに含まれる食塩の量を調べたいときは
- 式)300×0.08 = 24(g)
ではなく
- 式)3×8 = 24(g)
と計算します。
(3) 2つの食塩水に関する問題②・・・例題3
(2)の方法で解けない2つの食塩水に関する問題は、面積図を利用して問題を解きます。
![]()
<基本問題>
8%の食塩水を作るためには、食塩40gを何gの水に溶かせばよいか。
一種類の食塩水の食塩と水の内訳を問う問題は、食塩水の構造をイメージする。
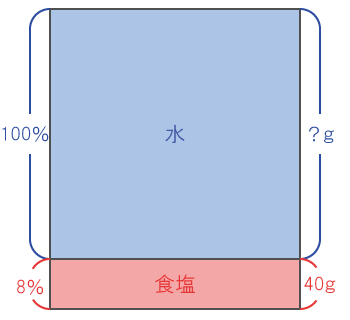
水を溶かした後にできる食塩水全体の重さは
- 式)40×(100 / 8)= 500(g)
そのうち水は
- 式)500 – 40 = 460(g)
である。
5%の食塩水100gと8%の食塩水200gを混ぜると何%の食塩水ができるか。
まず、両方の食塩水に入っている食塩の量を求める。
この問題は、食塩水の量がx00gのため、公式② [食塩水(g)/ 100]×[濃度(整数)] = 食塩(g)を利用する。
5%の食塩水100gと8%の食塩水200gに含まれる食塩の量は
- 式) 1×5 + 2×8 = 21(g)
である。また、食塩水の量の和は
- 式)100 + 200 = 300(g)
である。求める食塩水の濃度をa(%)とおくと、公式② [食塩水(g)/ 100]×[濃度(整数)] = 食塩(g)より
- 式)3×a = 21 これを解いて a = 7(%)
【面積図】
この問題では、公式で食塩の量を求められるため、面積図を利用する必要はない。
しかし、面積図に慣れてもらうため、面積図を用いた解説を紹介する。
下図が面積図である。
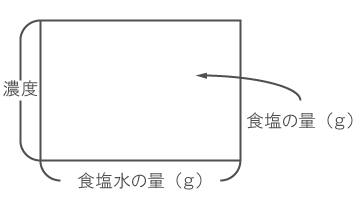
縦軸が濃度(%)、横軸が食塩水の量(g)、面積が食塩の量(g)である。
したがって、5%の食塩水100gと、8%の食塩水200gは下図のように描くことができる。
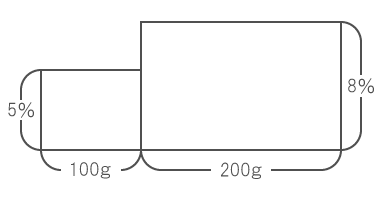
この2つを混ぜあわせると、量も濃度もある一定の量になる。
したがって、面積図で1つの四角形として描くことができる。
このとき、2つの食塩水を混ぜ合わせても、食塩の量は変わらないことを利用したのが下図である。
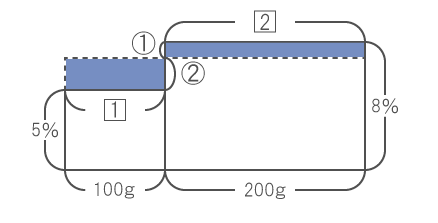
右上の青色部分の四角形を切り取り、左上の青色の四角形部分に持ってくる。
食塩の量は変わらないため、青色部分の四角形の面積は等しい。
2つの四角形の面積が等しいとき、縦の比と横の比は、逆比の関係になるため、青色の四角形の縦の部分は、上図のような比になる。
横が左から
- 式)100 : 200 = 1 : 2
になるため、縦は下から2 : 1になるというわけである。
5%と8%の差である3%が、2 : 1で分けられることになるので、新しくできた300gの食塩水の濃度は7%となる。
7%の食塩水200gに、17%の食塩水を混ぜて、13%の食塩水を作る。このとき、17%の食塩水を何g混ぜればよいか。
【面積図】
この問題は、公式を利用して食塩の量を直接求められないため、面積図(例題2の別解で説明)を描く。
問題として与えられた情報を面積図にすると、下図になる。
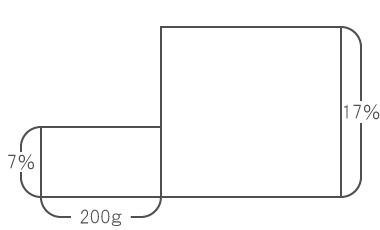
] 17%と7%の食塩水を混ぜて、13%の食塩水を作るため、四角形の縦の比は下から3 : 2である。
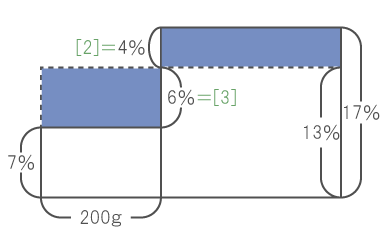
そのため、四角形の横の比は左から2 : 3となる。
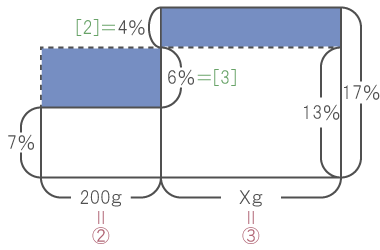
17%の食塩水の量をa(g)とすると
- 式)2 : 3 = 200 : a
が成り立つため、内項の積 = 外項の積より
- 式)3×200 = 2×a これを解いて a = 300(g)
面積図の考え方がしっくり来るようなこちらをオススメしたいですね!
とにかく速いですので!(*´∀`*)
【連立方程式】
17%の食塩水をA、13%の食塩水をBとおくと・・・
17%の食塩水の食塩は0.17A(g)
13%の食塩水の食塩は0.13B(g)
7%の食塩水の食塩は200×0.07(g)
・・・と表せる。
よって、以下の連立方程式が成り立つ。
200 + A = B・・・①
200×0.07 + 0.17A = 0.13B・・・②
①の右辺と左辺を入れ替えて
B = 200 + A・・・③
③を②に代入して・・・
200×0.07 + 0.17A = 0.13(200 + A)
0.04A = 12
A = 300(g)
方程式は慣れても頭で処理するのは困難(というか私は無理・・・)なので、少し時間がかかります(ノ∀`;)
とは言え、色々な問題に応用できるのが方程式の良いところでしょう!(*´∀`*)
食塩水を追加する
20gの食塩を水の入ったコップに溶かすと5%の食塩水ができた。コップには何gの水が入っていたか。
一種類の食塩水の食塩と水の内訳を問う問題は、食塩水の構造をイメージする。
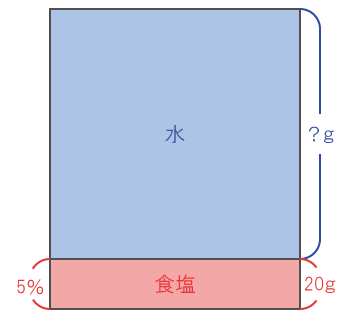
求める水の量は
- 式)20×(100 / 5) – 20 = 380(g)
食塩水を混ぜる
12%の食塩水400gと、16%の食塩水600gを混ぜると何%の食塩水ができるか。
まず、両方の食塩水に入っている食塩の量を求める。
この問題は、食塩水の量がx00gのため、公式② [食塩水(g)/ 100]×[濃度(整数)] = 食塩(g)を利用する。
12%の食塩水400gと16%の食塩水600gに含まれる食塩の量は
- 式)4×12 + 6×16 = 144(g)
である。また、食塩水の量の和は
- 式)400 + 600 = 1000(g)
である。求める食塩水の濃度をa(%)とおくと、公式② [食塩水(g)/ 100]×[濃度(整数)] = 食塩(g)より
- 式)10×a = 144 これを解いて a = 14.4(%)
水を追加する
15%の食塩水400gにある量の水を加えると食塩水の濃さが12%になった。加えた水の量は何gか。
始めの食塩水に含まれる食塩の量は、公式② [食塩水(g)/ 100]×[濃度(整数)] = 食塩(g)より
- 式)4×15 = 60(g)
水を加えても食塩の量は変わらないので、12%の食塩水に含まれる食塩の量も60gである。
この12%の食塩水の量をa(g)とおくと、公式① [食塩水(g)]×[濃度(小数)] = 食塩(g)より
- 式)a×0.12 = 60 これを解いて a = 500(g)
(食塩水の量を求めたい場合は、食塩水がx00gかどうか判断できないため、公式② [食塩水(g)/ 100]×[濃度(整数)] = 食塩(g)ではなく、公式① [食塩水(g)]×[濃度(小数)] = 食塩(g)を使います。)
したがって、加えた水の量は、
- 式)500 – 400 =100(g)
面積図・連立方程式
3%の食塩水と10%の食塩水を混ぜて、5%の食塩水を350g作りたい。このとき、3%の食塩水は何g必要か。
【面積図】
この問題は、公式を利用して食塩の量を直接求められないため、面積図(例題2の別解で説明)を描く。
問題として与えられた情報を面積図にすると、下図になる。
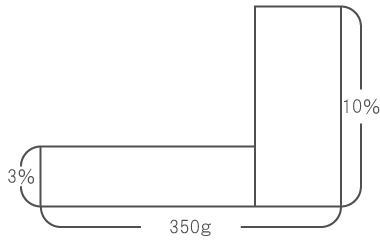
3%と10%の食塩水を混ぜて、5%の食塩水を作るため、四角形の縦の比は下から2 : 5である。
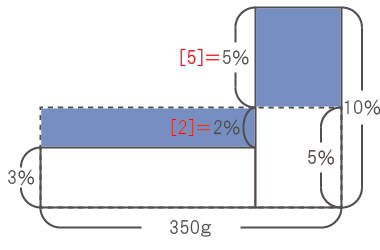
そのため、四角形の横の比は左から5 : 2となる。
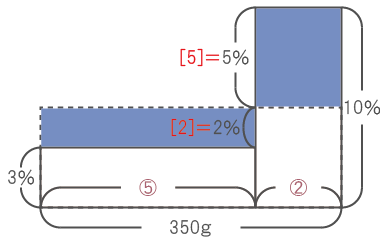
たがって、3%の食塩水は
- 式)350×{5 / (5 + 2)} = 250(g)
面積図の考え方がしっくり来るようなこちらをオススメしたいですね!
とにかく速いですので!(*´∀`*)
【連立方程式】
3%の食塩水をA、10%の食塩水をBとおくと・・・
3%の食塩水の食塩は0.03A(g)
10%の食塩水の食塩は0.10B(g)
5%の食塩水の食塩は350×0.10(g)
・・・と表せる。
よって、以下の連立方程式が成り立つ。
A + B = 350・・・①
0.03A + 0.10B = 350×0.05・・・②
①を変形して
B = 350 – A・・・③
③を②に代入して・・・
0.03A + 0.10(350 – A) = 350×0.05
– 0.07A = – 17.5
A = 250(g)
方程式は慣れても頭で処理するのは困難(というか私は無理・・・)なので、少し時間がかかります(ノ∀`;)
とは言え、色々な問題に応用できるのが方程式の良いところでしょう!(*´∀`*)
水を蒸発させる
15%の食塩水200gを24%にするためには、何gの水を蒸発させればよいか。
食塩水に含まれる食塩の量は、公式② [食塩水(g)/ 100]×[濃度(整数)] = 食塩(g)より
- 式)2×15 = 30(g)
水を蒸発させても食塩の量は変わらないため、水を蒸発させた後の24%の食塩水に含まれる食塩の量も30gである。
この24%の食塩水の量をa(g)とおくと、公式① [食塩水(g)]×[濃度(小数)] = 食塩(g)より
- 式)a×0.24 = 30 これを解いて a = 125(g)
したがって、蒸発させる水は
- 式)200 – 125 = 75(g)
3つの食塩水
15%の食塩水200gと18%の食塩水200gと20%の食塩水100gを混ぜ合わせると、何%の食塩水ができるか。
3つの食塩水に含まれる食塩の量の合計は、公式② [食塩水(g)/ 100]×[濃度(整数)] = 食塩(g)より
- 式)2×15 + 2×18 + 1×20 = 86(g)
3つの食塩水の量の合計は
- 式)200 + 200 + 100 = 500(g)
求める濃度をa(%)とおくと、公式① [食塩水(g)]×[濃度(小数)] = 食塩(g)より
- 式)5×a = 86(g) これを解いて a = 17.2(%)
