<ポイント>
少ない情報から「必ず正しいと推論できる事柄」を求めます。
情報を図式化したり、漏れなく挙げることでミスを防ぎましょう!!
- (1)発言の正誤を推論する問題・・・例題1
- → 各発言を詳しい順に並べよう!
- ※ 詳しい順に並べられない(互いに関係する情報がまったくない)発言もあります。
- (2)順位を推論する問題・・・例題2
- → 想定できる順位のパターンを全て洗い出そう!
- (3) 個数の内訳を推論する問題・・・例題3
- → 与えられた情報から、想定できる個数のパターンを全て列挙しよう!
- (4) 平均から値段や得点を推論する問題・・・例題4
- → 平均から合計を求めよう!(2個の平均の値段が100円 → 2個の合計の値段は200円)
- (5) 人口密度や食塩水の濃度を推論する問題・・・例題5
- → 問題文に「2倍」や「半分」など、比率に関するキーワードがある!「比率」から「実際の値」を仮定して解こう!
- (6) 対戦成績を推論する問題・・・問題6-1
- → 与えられた情報を対戦表に書き出そう!
- (7) 位置関係を推論する問題・・・問題8-1、問題9-1
- → 想定できる位置関係のパターンを全て洗い出そう!
- (8) 必要な条件を推論する問題・・・問題10-1
- → 提示された条件について、まず1つの条件だけで設問の答えが決まるかを洗い出そう!
決まらなければ、2つ、3つの条件で・・・と条件を追加して考えよう!
![]()
<基本問題>
52枚1組のトランプから、カードが1枚配られた。この1枚のカードについて、次の発言があった。
- ⅰ)配られたカードは、ハートの5ではなかった
- ⅱ)配られたカードは、ハートではなかった
- ⅲ)配られたカードは、スペードの5であった
ⅰ)~ⅲ)までの発言は信頼できるとは限らない。そこで、いろいろな場合を想定して推論がなされた。
- (1)次のア、イ、ウの推論のうち、正しいのはどれか。
- アⅰ)が正しければ、ⅱ)も必ず正しい
- イⅱ)が正しければ、ⅲ)も必ず正しい
- ウⅲ)が正しければ、ⅰ)も必ず正しい
- Aアだけ
- Bイだけ
- Cウだけ
- Dアとイの両方
- Eアとウの両方
- Fイとウの両方
- Gアとイとウのすべて
- H正しい推論はない
- (2)次のカ、キ、クの推論のうち、正しいのはどれか。
- カⅰ)が正しければ、ⅲ)も必ず正しい
- キⅱ)が正しければ、ⅰ)も必ず正しい
- クⅲ)が正しければ、ⅱ)も必ず正しい
- Aカだけ
- Bキだけ
- Cクだけ
- Dカとキの両方
- Eカとクの両方
- Fキとクの両方
- Gカとキとクのすべて
- H正しい推論はない
練習01
発言の正誤を推論する問題は、各発言を詳しい順に並べる。
発言ⅰ)~ⅲ)によって、配られたトランプの取りうる範囲は、下図のように変わる。
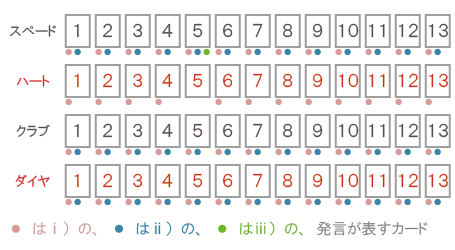
よって、各発言を「詳しい順」に並べると
ⅲ)「スペードの5」
ⅱ)「ハート以外」
ⅰ)「ハートの5以外」
ある発言が正しければ、それよりも詳しくない発言は必ず正しいので
「ⅲ)が正しい → ⅱ)とⅰ)は必ず正しい」
「ⅱ)が正しい → ⅰ)は必ず正しい」
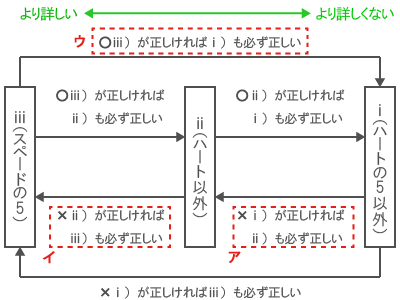
したがって、正しい推論はウだけ。
(1)でまとめた図の通りである。
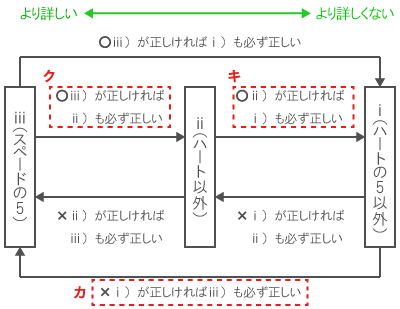
したがって、正しい推論はキとクの両方。
なお、テストセンターSPIでは、このように「組問題」で出題される。
そのため、あらかじめ全ての発言の関係を洗い出しておくと、結果的に素早く解くことができる。
練習02
P、Q、R、Sの4人で徒競走をした。4人のタイムや順位について次のことが分かっている。
- ⅰ)Qのタイムは、RとSのタイムの平均である
- ⅱ)Pの順位は、Rより上である
- ⅲ)同着の順位のものはいない
- (1)次のア、イ、ウの推論のうち、必ず正しいものはどれか。
- ア1位はPかSである
- イ2位はQかRかSである
- ウ4位はRかSである
- Aアだけ
- Bイだけ
- Cウだけ
- Dアとイの両方
- Eアとウの両方
- Fイとウの両方
- Gアとイとウのすべて
- H必ず正しい推論はない
- (2)ⅰ)、ⅱ)、ⅲ)に、「ⅳ) Pの順位はSよりも高い」という情報が加わった。このとき、次のカ、キ、クの推論のうち、必ず正しいものはどれか。
- カ1位はPである
- キ3位はQである
- ク4位はSである
- Aカだけ
- Bキだけ
- Cクだけ
- Dカとキの両方
- Eカとクの両方
- Fキとクの両方
- Gカとキとクのすべて
- H必ず正しい推論はない
順位を推論する問題は、与えられた情報から、想定できる順位のパターンを全て洗い出す。
下記のルールにしたがって、与えられた情報を図式化する。
「順位の高低関係のみ」を表現するときは、「[ 順位がより高い方 ] > [ 順位がより低い方 ]」と表す。
「連続する順位の並び」を表現するときは、「[ 順位が高い方 ] → [ 順位が低い方 ]」と表す。
このルールにしたがって、問題文の情報を図式化すると
ⅰ)「Qのタイムは、RとSのタイムの平均である」とⅲ)「同着の順位のものはいない」より、QとRとSの関係は、「R > Q > S」または「S > Q > R」・・・①
ⅱ)「Pの順位は、Rより上である」より、PとRの関係は、「P > R」・・・②
①が「R > Q > S」の場合は、②の「P > R」と合わせて考えると、4人の順位は、「P → R → Q → S」となる。
一方、①が「S > Q > R」の場合は、②の「P > R」と合わせて考えると、4人の順位は、「P → S → Q → R」「S → P → Q → R」「S → Q → P → R」の3通りの関係が考えられる。
よって、考えられる順位は、次の4通りである。
| 順位 | ||||
| 1位 | 2位 | 3位 | 4位 | |
| パターン1 | P | R | Q | S |
| パターン2 | P | S | Q | R |
| パターン3 | S | P | Q | R |
| パターン4 | S | Q | P | R |
ここで、推論ア~ウについて考えると
表より、1位はPかSである。よって、ア「1位はPかSである」は必ず正しい。
表より、2位はPかQかRかSである。よって、イ「2位はQかRかSである」は正しいとは限らない。
表より、4位はRかSである。よって、ウ「4位はRかSである」は必ず正しい。
したがって、正しい推論はアとウの両方。
ⅳ)「Pの順位はSよりも高い」より、PとSの関係は、「P > S」・・・④
④により、(1)でまとめた表のパターン3、4は候補から外れ、パターン1、2が残る。
| 順位 | ||||
| 1位 | 2位 | 3位 | 4位 | |
| パターン1 | P | R | Q | S |
| パターン2 | P | S | Q | R |
ここで、推論カ~クについて考えると
表より、1位はPである。よって、カ「1位はPである」は必ず正しい。
表より、3位はQである。よって、キ「3位はQである」は必ず正しい。
表より、4位はRかSである。よって、ウ「4位はSである」は正しいとは限らない。
したがって、正しい推論はカとキの両方。
練習03
青玉、黄玉、赤玉が合わせて8個ある。それぞれの個数について次のことが分かっている。
- ⅰ)青玉、黄玉、赤玉は、それぞれ少なくとも1個はある
- ⅱ)黄玉の数は青玉より少ない
- (1)次のア、イ、ウの推論のうち、必ず正しいものはどれか。
- ア青玉が3個であれば、黄玉は2個である
- イ黄玉が3個であれば、赤玉は1個である
- ウ赤玉が3個であれば、青玉は4個である
- Aアだけ
- Bイだけ
- Cウだけ
- Dアとイの両方
- Eアとウの両方
- Fイとウの両方
- Gアとイとウのすべて
- H必ず正しい推論はない
- (2)次のカ、キ、クの推論のうち、必ず正しいものはどれか。
- カ青玉と赤玉の個数が同じであれば、黄玉は2個である
- キ黄玉と赤玉の個数が同じであれば、青玉は4個である
- ク赤玉が4個であれば、青玉は3個である
- Aカだけ
- Bキだけ
- Cクだけ
- Dカとキの両方
- Eカとクの両方
- Fキとクの両方
- Gカとキとクのすべて
- H必ず正しい推論はない
個数の内訳を推論する問題は、与えられた情報から、想定できる個数のパターンを全て列挙する。
ⅰ)「青玉、黄玉、赤玉は、それぞれ少なくとも1個はある」
ⅱ)「黄玉の数は青玉より少ない」より
個数の組合せパターンは以下の9通りが考えられる。
[青玉,黄玉,赤玉] = [6,1,1]、[5,2,1]、[5,1,2]、[4,3,1]、[4,2,2]、[4,1,3]、[3,2,3]、[3,1,4]、[2,1,5]
組合せのパターンを列挙するときは、漏れをなくすために「列挙するル-ル」が必要。
この解説では、青玉が多い順番 ⇒ 黄玉が多い順番、というルールで列挙する。
では、推論ア~ウについて考えていこう。
ア青玉が3個であれば、黄玉は2個である → 正しいとは限らない。
上の9通りのうち、アの「青玉が3個」という条件を満たすものは以下の2通りである。
[青玉,黄玉,赤玉] = [3,2,3]、[3,1,4]
よって、ア「青玉が3個であれば、黄玉は2個である」は正しいとは限らない。
イ黄玉が3個であれば、赤玉は1個である → 必ず正しい。
上の9通りのうち、イの「黄玉が3個」という条件を満たすものは以下の1通りである。
[青玉,黄玉,赤玉] = [4,3,1]
よって、イ「黄玉が3個であれば、赤玉は1個である」は必ず正しい。
ウ赤玉が3個であれば、青玉は4個である → 正しいとは限らない。
上の9通りのうち、ウの「赤玉が3個」という条件を満たすものは以下の2通りである。
[青玉,黄玉,赤玉] = [4,1,3]、[3,2,3]
よって、ウ「赤玉が3個であれば、青玉は4個である」は正しいとは限らない。
(1)の解説の最初でまとめた9通りの組合せパターンをもとに、推論カ~クについても考えていこう。
[青玉,黄玉,赤玉] = [6,1,1]、[5,2,1]、[5,1,2]、[4,3,1]、[4,2,2]、[4,1,3]、[3,2,3]、[3,1,4]、[2,1,5]
カ青玉と赤玉の個数が同じであれば、黄玉は2個である → 必ず正しい。
上の9通りのうち、カの「青玉と赤玉の個数が同じ」という条件を満たすものは以下の1通りである。
[青玉,黄玉,赤玉] = [3,2,3]
よって、カ「青玉と赤玉の個数が同じであれば、黄玉は2個である」は必ず正しい。
キ黄玉と赤玉の個数が同じであれば、青玉は4個である → 正しいとは限らない。
上の9通りのうち、キの「黄玉と赤玉の個数が同じ」という条件を満たすものは以下の2通りである。
[青玉,黄玉,赤玉] = [6,1,1]、[4,2,2]
よって、キ「黄玉と赤玉の個数が同じであれば、青玉は4個である」は正しいとは限らない。
ク赤玉が4個であれば、青玉は3個である → 必ず正しい。
上の9通りのうち、クの「赤玉が4個」という条件を満たすものは以下の1通りである。
[青玉,黄玉,赤玉] = [3,1,4]
よって、ク「赤玉が4個であれば、青玉は3個である」は必ず正しい。
練習04
P、Q、Rの商品の価格について、次のことが分かっている。
- ⅰ)PとQの価格の平均額は7000円である
- ⅱ)QとRの価格の平均額は9000円である
次のア、イ、ウの推論のうち、必ず正しいものはどれか。
- アQの価格は、Pの価格より高い
- イRの価格は、Pの価格より高い
- ウRの価格は、Qの価格より高い
- Aアだけ
- Bイだけ
- Cウだけ
- Dアとイの両方
- Eアとウの両方
- Fイとウの両方
- Gアとイとウのすべて
- H必ず正しい推論はない
平均から値段や得点を推論する問題は、まず平均から合計を求める。
ⅰ)「PとQの価格の平均額は7000円である」より、PとQの価格の合計を求める。
- 式)P + Q = 7000×2 = 14000(円)・・・①
ⅱ)「QとRの価格の平均額は9000円である」より、QとRの価格の合計を求める。
- 式)Q + R = 9000×2 = 18000(円)・・・②
② – ①より
- – ) – P +Q + R = 18000
– ) -P + Q+ R= 14000
– )- P+ Q+ R = 4000
– ) – P + Q +R = P + 4000
したがって、Rの価格はPより4000円高い。・・・③
では、推論ア~ウについて考えていこう。
アQの価格は、Pの価格より高い → 正しいとは限らない。
①より、PとQの価格の合計は14000円であることが分かっているが、どちらが高いかは分かっていない。
例えば、P = 1000円、Q = 13000円ということもあり得る。
よって、ア「Qの価格は、Pの価格より高い」は正しいとは限らない。
イRの価格は、Pの価格より高い → 必ず正しい。
③より、Rの価格はPより4000円高いことが分かっている。
よって、イ「Rの価格は、Pの価格より高い」は必ず正しい。
ウRの価格は、Qの価格より高い → 正しいとは限らない。
②より、QとRの価格の合計は18000円であることが分かっているが、どちらが高いかは分かっていない。
例えば、Q = 13000円、R = 5000円ということもあり得る。
よって、ウ「Rの価格は、Qの価格より高い」は正しいとは限らない。
練習05
P市、Q市、R市の人口密度(面積1km2当たりの人口)は下表の通りである。P市とQ市の面積は等しく、それぞれR市の面積の半分である。
| 市 | 人口密度 |
| P | 200 |
| Q | 180 |
| R | 120 |
次のア、イの正誤を考え、AからIまでの中から正しいものを1つ選びなさい。
- アP市の人口はR市より少ない
- イQ市とR市を合わせた人口密度は135である
- Aアもイも正しい
- Bアは正しいが、イは分からない
- Cアは正しいが、イは誤り
- Dアは分からないが、イは正しい
- Eアもイも分からない
- Fアは分からないが、イは誤り
- Gアは誤りだが、イは正しい
- Hアは誤りだが、イは分からない
- Iアもイも誤り
人口密度や食塩水の濃度を推論する問題では、問題文に「2倍」や「半分」など、比率に関するキーワードがある。 「比率」から「実際の値」を仮定して問題を解く。
問題文には「P市とQ市の面積は等しく、それぞれR市の面積の半分である」とあるため、 P市、Q市の面積を1km2、R市の面積を2km2と仮定して、それぞれの市の人口を次の式で求める。
[ 人口(人) ] = [ 人口密度(人 / km2) ]×[ 面積(km2) ]
| 市 | 人口密度 | 面積 | 人口 |
| P | 200人 / km2 | 1km2 | 200人 |
| Q | 180人 / km2 | 1km2 | 180人 |
| R | 120人 / km2 | 2km2 | 240人 |
上表をもとに、推論ア、イについて考えていこう。
アP市の人口はR市より少ない → 正しい。
表より、P市の人口は200人、R市の人口は240人である。
よって、ア「P市の人口はR市より少ない」は正しい。
イQ市とR市を合わせた人口密度は135である → 誤り。
Q市とR市の人口密度は
- 式)[ 人口密度(人 / km2) ] = [ 人口(人) ]÷[ 面積(km2) ]
= (180 + 240)÷(1 + 2)
= 420÷3
= 140(人 / km2)
よって、イ「Q市とR市を合わせた人口密度は135である」は誤り。
![]()
Q1、順位
P、Q、R、S、Tの5人で徒競走をした。5人の順位について次のことが分かっている。
- ⅰ)Rの順位は、Sより上である
- ⅱ)Tの順位は、Rよりも上だが、1着ではなかった
- ⅲ)Qの順位は、Pより上である
- ⅳ)同着の順位の者はいない
- (1)次のア、イ、ウの推論のうち、必ず正しいものはどれか。
- アQは1着である
- イSは5着である
- ウ2着はPまたはTである
▼ 選択肢をクリックすると、採点して解答を表示します。
| Aアだけ |
| Bイだけ |
| Cウだけ |
| Dアとイの両方 |
| Eアとウの両方 |
| Fイとウの両方 |
| Gアとイとウのすべて |
| H必ず正しい推論はない |
順位を推論する問題は、与えられた情報から、想定できる順位のパターンを全て洗い出す。
下記のルールにしたがって、与えられた情報を図式化する。
「順位の高低関係のみ」を表現するときは、「[ 順位がより高い方 ] > [ 順位がより低い方 ]」と表す。
「連続する順位の並び」を表現するときは、「[ 順位が高い方 ] → [ 順位が低い方 ]」と表す。(ただし、この問題では使わない。)
このルールにしたがって、問題文の情報を図式化する。
ⅰ)「Rの順位は、Sより上である」より、RとSの順位関係は、「R > S」・・・①
ⅱ)「Tの順位は、Rよりも上だが、1着ではなかった」より、TとRの順位関係は、「□ > T > R」・・・②
①、②より、「□ > T > R > S」・・・③
ⅲ)「Qの順位は、Pより上である」より、「Q > P」・・・④
③、④より、考えられる順位は、次の4通りである。
| 順位 | |||||
| 1位 | 2位 | 3位 | 4位 | 5位 | |
| パターン1 | Q | P | T | R | S |
| パターン2 | Q | T | P | R | S |
| パターン3 | Q | T | R | P | S |
| パターン4 | Q | T | R | S | P |
ここで、推論ア~ウについて考えると
表より、1着はQである。よって、ア「Qは1着である」は必ず正しい。
表より、5着はSかPである。よって、イ「Sは5着である」は正しいとは限らない。
表より、2着はPまたはTである。よって、ウ「2着はPまたはTである」は必ず正しい。
したがって、正しい推論はアとウの両方。
Q2、順位2
P、Q、R、S、Tの5人で徒競走をした。5人の順位について次のことが分かっている。
- ⅰ)Rの順位は、Sより上である
- ⅱ)Tの順位は、Rよりも上だが、1着ではなかった
- ⅲ)Qの順位は、Pより上である
- ⅳ)同着の順位の者はいない
(2)更にどのような情報が追加されれば、5人の着順が全て決まるか。ただし、情報として追加する選択肢は、できる限り抑えるものとする。
- カTは2番目に到着した
- キRは3番目に到着した
- クSは4番目に到着した
| Aカだけ |
| Bキだけ |
| Cクだけ |
| Dカとキの両方 |
| Eカとクの両方 |
| Fキとクの両方 |
| Gカとキとクのすべて |
| Hカとキとクのすべてが追加されても分からない |
(1)でまとめた表を元に、追加される情報カ~クについて考える。
| 順位 | |||||
| 1位 | 2位 | 3位 | 4位 | 5位 | |
| パターン1 | Q | P | T | R | S |
| パターン2 | Q | T | P | R | S |
| パターン3 | Q | T | R | P | S |
| パターン4 | Q | T | R | S | P |
表より、Tが2着であるパターンは3つあるため、カ「Tは2番目に到着した」だけでは全ての着順は決まらない。
表より、Rが3着であるパターンは2つあるため、キ「Rは3番目に到着した」だけでは全ての着順は決まらない。
表より、Sが4着であるパターンは1つしかないため、ク「Sは4番目に到着した」だけで全ての着順が決まる。
したがって、クだけ追加されれば、5人の着順が全て決まる。
Q3、発言の正誤
ある企業のグローバル化推進部のメンバーについて、次の3つの情報があった
- ⅰ)少なくとも2ヵ国のヨーロッパ国籍のメンバーがいる。
- ⅱ)少なくともイタリア国籍が2人とスペイン国籍が2人いる。
- ⅲ)少なくとも3人のヨーロッパ国籍のメンバーがいる。
ⅰ)~ⅲ)までの情報は信頼できるとは限らない。そこで、いろいろな場合を想定して推論がなされた。
- (1)次のア、イ、ウの推論のうち、正しいのはどれか。
- アⅰ)が正しければ、ⅱ)も必ず正しい
- イⅱ)が正しければ、ⅲ)も必ず正しい
- ウⅲ)が正しければ、ⅰ)も必ず正しい
各情報の関係性を整理する。
この問題に限らず、推論の問題は「落ち着けば誰でも解けるものばかり」。
スピードを少し落としても、確実に得点したい。
今回は、下表の赤点線の3つの部分しか問われていないが、組問題で(2)が出題された場合は、残り3つの関係性を問われることになるので、最初に洗い出しておくとラク!(*´∀`*)
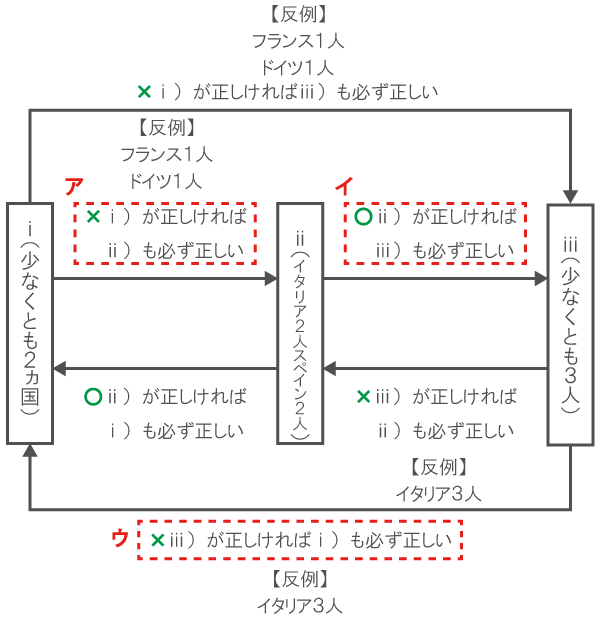
1個でも反例が見つかれば「必ず正しい推論」ではない!
反例を素早く見つけるために、極端な例を思い浮かべるようにしよう!
したがって、正しい推論はイのみ。
なお、時間効率を考慮して、当サイトでは以下、問題(2)の解説は掲載せず、次に進みます。(*´∀`*)
組問題として出題される、ということだけ押さえておきましょう。
- (2)次のカ、キ、クの推論のうち、正しいのはどれか。
- カⅱ)が正しければ、ⅰ)も必ず正しい
- キⅲ)が正しければ、ⅱ)も必ず正しい
- クⅰ)が正しければ、ⅲ)も必ず正しい
Q4,発言の正誤2
コインを5回投げて表と裏の回数を数えた。この結果として次の情報があった。
- ⅰ)表が出た回数は3回である
- ⅱ)裏が出た回数の方が少ない
- ⅲ)裏が出た回数は偶数である
ⅰ)~ⅲ)までの発言は信頼できるとは限らない。そこで、いろいろな場合を想定して推論がなされた。
- (1)次のア、イ、ウの推論のうち、正しいのはどれか。
- アⅰ)が正しければ、ⅱ)も必ず正しい
- イⅱ)が正しければ、ⅲ)も必ず正しい
- ウⅲ)が正しければ、ⅰ)も必ず正しい
各情報の関係性を整理する。
今回は、下表の赤点線の3つの部分しか問われていないが、組問題で(2)が出題された場合は、残り3つの関係性を問われることになるので、最初に洗い出しておくとラク!(*´∀`*)
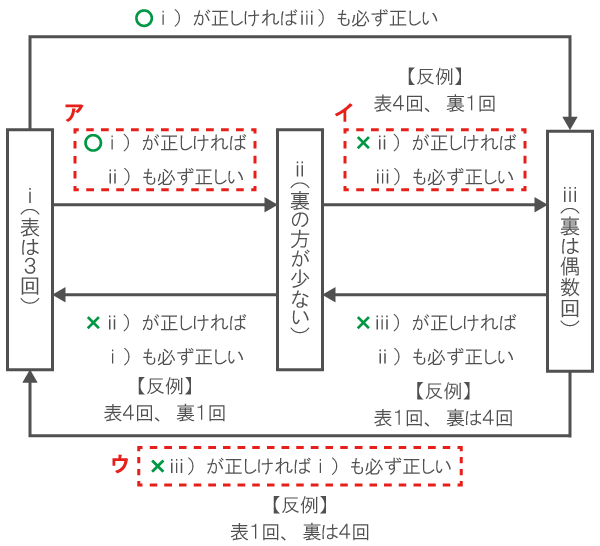
したがって、正しい推論はア。
なお、時間効率を考慮して、当サイトでは以下、問題(2)の解説は掲載せず、次に進みます。(*´∀`*)
組問題として出題される、ということだけ押さえておきましょう。
- (2)次のカ、キ、クの推論のうち、正しいのはどれか。
- カⅱ)が正しければ、ⅰ)も必ず正しい
- キⅲ)が正しければ、ⅱ)も必ず正しい
- クⅰ)が正しければ、ⅲ)も必ず正しい
Q5,内訳
リンゴとミカンとブドウを全部で9個買った。それぞれの個数について次のことが分かっている。
- ⅰ)それぞれの果物を少なくとも1個は買った
- ⅱ)リンゴの数はミカンより多い
- (1)次のア、イ、ウの推論のうち、必ず正しいものはどれか。
- アリンゴが3個であれば、ミカンは2個である
- イミカンが3個であれば、ブドウは2個である
- ウブドウが6個であれば、リンゴは2個である
個数の内訳を推論する問題は、与えられた情報から、想定できる個数のパターンを全て列挙する。
ⅰ)「それぞれの果物を少なくとも1個は買った」
ⅱ)「リンゴの数はミカンより多い」
より、個数の組合せパターンは以下の12通りが考えられる。
[リンゴ,ミカン,ブドウ] = [7,1,1]、[6,2,1]、[6,1,2]、[5,3,1]、[5,2,2]、[5,1,3]、[4,3,2]、[4,2,3]、[4,1,4]、[3,2,4]、[3,1,5]、[2,1,6]
組合せのパターンを列挙するときは、漏れをなくすために「列挙するルール」が必要。
この解説では、リンゴが多い順番 ⇒ ミカンが多い順番、というルールで列挙する。
では、推論ア~ウについて考えていこう。
アリンゴが3個であれば、ミカンは2個である → 正しいとは限らない。
上の12通りのうち、アの「リンゴが3個」という条件を満たすものは以下の2通りである。
[リンゴ,ミカン,ブドウ] = [3,2,4]、[3,1,5]
よって、ア「リンゴが3個であれば、ミカンは2個である」は正しいとは限らない。
イミカンが3個であれば、ブドウは2個である → 正しいとは限らない。
上の12通りのうち、イの「ミカンが3個」という条件を満たすものは以下の2通りである。
[リンゴ,ミカン,ブドウ] = [5,3,1]、[4,3,2]
よって、イ「ミカンが3個であれば、ブドウは2個である」は正しいとは限らない。
ウブドウが6個であれば、リンゴは2個である → 必ず正しい。
上の12通りのうち、ウの「ブドウが6個」という条件を満たすものは以下の1通りである。
[リンゴ,ミカン,ブドウ] = [2,1,6]
よって、ウ「ブドウが6個であれば、リンゴは2個である」は必ず正しい。
ケアレスミスを防止できるため、当サイトでは、最初に全てのパターンを列挙する解法をお薦めしている。
しかし、この問題のように、条件によって想定できる個数のパターンが多い場合は、あらかじめ全てを列挙せずに、推論ア~ウに含まれている条件を考慮して、直接解いた方が素早く解けることもある。
臨機応変に対応してほしい。
Q6、内訳2
リンゴとミカンとブドウを全部で9個買った。それぞれの個数について次のことが分かっている。
- ⅰ)それぞれの果物を少なくとも1個は買った
- ⅱ)リンゴの数はミカンより多い
- (2)次のカ、キ、クの推論のうち、必ず正しいものはどれか。
- カリンゴが3個以下であれば、ブドウは4個以上である
- キミカンの数がブドウより多ければ、ブドウは1個である
- クミカンとブドウの個数が同じであれば、リンゴは7個である
(1)の解説の最初でまとめた12通りの組合せパターンをもとに、推論カ~クについても考えていこう。
[リンゴ,ミカン,ブドウ] = [7,1,1]、[6,2,1]、[6,1,2]、[5,3,1]、[5,2,2]、[5,1,3]、[4,3,2]、[4,2,3]、[4,1,4]、[3,2,4]、[3,1,5]、[2,1,6]
カリンゴが3個以下であれば、ブドウは4個以上である → 必ず正しい。
上の12通りのうち、カの「リンゴが3個以下」という条件を満たすものは以下の3通りである。
[リンゴ,ミカン,ブドウ] = [3,2,4]、[3,1,5]、[2,1,6]
よって、カ「リンゴが3個以下であれば、ブドウは4個以上である」は必ず正しい。
キミカンの数がブドウより多ければ、ブドウは1個である → 正しいとは限らない。
上の12通りのうち、キの「ミカンの数がブドウより多い」という条件を満たすものは以下の3通りである。
[リンゴ,ミカン,ブドウ] = [6,2,1]、[5,3,1]、[4,3,2]
よって、キ「ミカンの数がブドウより多ければ、ブドウは1個である」は正しいとは限らない。
クミカンとブドウの個数が同じであれば、リンゴは7個である → 正しいとは限らない。
上の12通りのうち、クの「ミカンとブドウの個数が同じ」という条件を満たすものは以下の2通りである。
[リンゴ,ミカン,ブドウ] = [7,1,1]、[5,2,2]
よって、ク「ミカンとブドウの個数が同じであれば、リンゴは7個である」は正しいとは限らない。
Q7、平均
P、Q、Rが100点満点のテストを受けた。得点について次のことが分かっている。
- ⅰ)PとQの平均得点は80点である
- ⅱ)PとQとRの平均得点は85点である
- (1)次のア、イ、ウの推論のうち、必ずしも誤りとはいえない推論はどれか。ただし、同点の者はいないものとする。
- ア3人の中で最も得点が高かったのはPである
- イ3人の中で最も得点が低かったのはQである
- ウ3人の中で最も得点が低かったのはRである
平均から値段や得点を推論する問題は、まず平均から合計を求める。
ⅰ)「PとQの平均得点は80点である」より、PとQの得点の合計を求める。
- 式)P + Q = 80×2 = 160(点)・・・①
ⅱ)「PとQとRの平均得点は85点である」より、PとQとRの得点の合計を求める。
- 式)P + Q + R = 85×3 = 255(点)・・・②
② – ①より、Rの得点を求める。
- – )P + Q + R = 255
– ) P + Q+ R= 160
– ) P + Q +R = 95(点)・・・③
では、推論ア~ウについて考えていこう。
必ずしも誤りとはいえない推論を見つけるためには、1つでも正しい例を挙げればよい。
ア3人の中で最も得点が高かったのはPである → 必ずしも誤りとはいえない。
①、②から、Pの得点を1つに決めることはできないが、例として、P = 100点、Q = 60点、R = 95点というパターンが挙げられる。
よって、ア「3人の中で最も得点が高かったのはPである」は必ずしも誤りとはいえない。
イ3人の中で最も得点が低かったのはQである → 必ずしも誤りとはいえない。
①、②から、Qの得点を1つに決めることはできないが、例として、P = 100点、Q = 60点、R = 95点というパターンが挙げられる。
よって、イ「3人の中で最も得点が低かったのはQである」は必ずしも誤りとはいえない。
ウ3人の中で最も得点が低かったのはRである → 必ず誤り。
③より、Rの得点は95点であることが分かっている。
そのため、この推論が正しい場合があるとすれば、それはPとQのいずれも、96点以上の得点である場合である。
しかし、前提条件であるⅰ)「PとQの平均得点は80点である」を考えると、そのようなケースはあり得ない。
よって、ウ「3人の中で最も得点が低かったのはRである」は必ず誤り。
Q8、平均2
P、Q、Rが100点満点のテストを受けた。得点について次のことが分かっている。
- ⅰ)PとQの平均得点は80点である
- ⅱ)PとQとRの平均得点は85点である
- (2) ⅰ)、ⅱ)に、「ⅲ) QとRの平均得点は90点である」という情報が加わった。 このとき、Pの得点は何点か?
(1)で以下の内容が分かっている。
- 式)P + Q + R = 85×3 = 255(点)・・・②
新しい情報である、ⅲ)「QとRの平均得点は90点である」より、QとRの得点の合計を求める。
- 式)Q + R = 90×2 = 180(点)・・・④
(1)で求めた② – ④より、Pの得点を求める。
- – )P + Q + R = 255
– ) P +Q + R = 180
– )P+ Q + R= 75(点)
Q9、比率
食塩水P、Q、Rの濃度は下表の通りである。PとQの食塩水の量は等しく、Rの食塩水の量はPの2倍である。
| 食塩水 | 濃度 |
| P | 9.0% |
| Q | 27.0% |
| R | 18.0% |
- (1)次のア、イの正誤を考え、AからIまでの中から正しいものを1つ選びなさい。
- アRに含まれる食塩の量は、Qに含まれる食塩の量より少ない
- イPとRを混ぜると濃度は15%になる
人口密度や食塩水の濃度を推論する問題では、問題文に「2倍」や「半分」など、比率に関するキーワードがある。 「比率」から「実際の値」を仮定して問題を解く。
問題文には「PとQの食塩水の量は等しく、Rの食塩水の量はPの2倍である」とあるため、 P、Qの量を100g、Rの量を200gと仮定して、それぞれの食塩の量を次の式で求める。
[ 食塩の量(g) ] = [ 食塩水の量(g) ]×[ 濃度(%) ]÷100
| 食塩水 | 濃度 | 食塩水の量 | 食塩の量 |
| P | 9.0% | 100g | 9g |
| Q | 27.0% | 100g | 27g |
| R | 18.0% | 200g | 36g |
上表をもとに、推論ア、イについて考えていこう。
アRに含まれる食塩の量は、Qに含まれる食塩の量より少ない → 誤り。
表より、Qに含まれる食塩の量は27g、Rに含まれる食塩の量は36gである。
よって、ア「Rに含まれる食塩の量は、Qに含まれる食塩の量より少ない」は誤り。
イPとRを混ぜると濃度は15%になる → 正しい。
PとRを混ぜたときの濃度は
- 式)[ 濃度(%) ] = [ 食塩の量(g) ]÷[ 食塩水の量(g) ]×100
= (9 + 36)÷(100 + 200)×100
= 45÷300×100
= 15(%)
よって、イ「PとRを混ぜると濃度は15%になる」は正しい。
Q10、比率2
食塩水P、Q、Rの濃度は下表の通りである。PとQの食塩水の量は等しく、Rの食塩水の量はPの2倍である。
| 食塩水 | 濃度 |
| P | 9.0% |
| Q | 27.0% |
| R | 18.0% |
- (2)次のカ、キの正誤を考え、AからIまでの中から正しいものを1つ選びなさい。
- カPとQに含まれる食塩の量の和は、Rに含まれる食塩の量と同じである
- キRの食塩水から水だけを蒸発させて半分の量にすると、Pの濃度と同じになる
(1)でまとめた表を使って、推論カ、キについて考えていこう。
| 食塩水 | 濃度 | 食塩水の量 | 食塩の量 |
| P | 9.0% | 100g | 9g |
| Q | 27.0% | 100g | 27g |
| R | 18.0% | 200g | 36g |
カPとQに含まれる食塩の量の和は、Rに含まれる食塩の量と同じである → 正しい。
PとQに含まれる食塩の量の和は
- 式)9 + 27 = 36(g)
よって、カ「PとQに含まれる食塩の量の和は、Rに含まれる食塩の量と同じである」は正しい。
キRの食塩水から水だけを蒸発させて半分の量にすると、Pの濃度と同じになる → 誤り。
食塩水から水だけを蒸発させて半分の量にするため、食塩の量は変わらず36gで、食塩水の量が100g(半分)になる。
そのため、水を蒸発させた後の、Rの濃度は
- 式)[ 濃度(%) ] = [ 食塩の量(g) ]÷[ 食塩水の量(g) ]×100
= 36÷100×100
= 36(%)
よって、キ「Rの食塩水から水だけを蒸発させて半分の量にすると、Pの濃度と同じになる」は誤り。
Q11、総当たり
P、Q、R、Sの4チームが、バスケットボールの試合を総当たり戦で行った。その試合結果について、次のことが分かっている。
- ⅰ)Pは2勝1敗だった
- ⅱ)PはQに勝った
- ⅲ)RはPに勝った
- ⅳ)SはQに勝った
- ⅴ)引き分けの試合は無かった
- (1)次のア、イ、ウの推論のうち、必ずしも誤りとはいえない推論はどれか。
- アQは1勝2敗だった
- イRは全勝だった
- ウSは全勝だった
対戦成績を推論する問題は、まず与えられた情報を対戦表にまとめる。
問題文より、分かっていることを対戦表にまとめる。
まず、表にそのまま書き込める情報を書き込んでいく。
この問題では
ⅱ)「PはQに勝った」
ⅲ)「RはPに勝った」
ⅳ)「SはQに勝った」
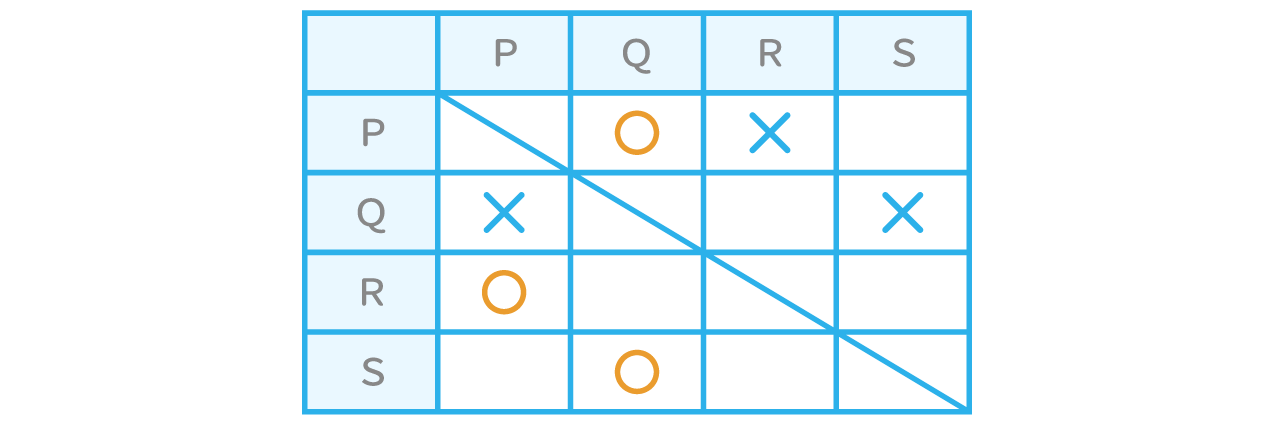
ⅰ)「Pは2勝1敗だった」より、Pは残ったSとの試合には勝ったことが分かる。
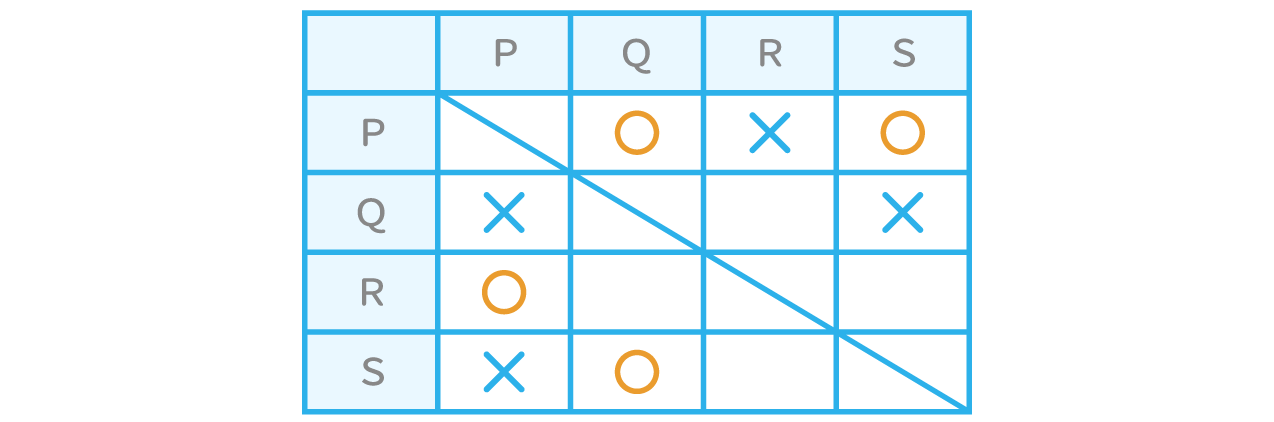
上表で、空欄部分は問題文の情報では分からなかった試合結果である。上表をもとに、推論ア、イ、ウについて考えていこう。
必ずしも誤りとはいえない推論を見つけるためには、1つでも正しい例を挙げればよい。
アQは1勝2敗だった → 必ずしも誤りとはいえない。
表の空欄「Q対R」がQの勝ちである場合、Qは1勝2敗である。
よって、ア「Qは1勝2敗だった」は必ずしも誤りとはいえない。
イRは全勝だった → 必ずしも誤りとはいえない。
表の空欄「R対Q」「R対S」が、いずれもRの勝ちである場合、Rは全勝である。
よって、イ「Rは全勝だった」は必ずしも誤りとはいえない。
ウSは全勝だった → 必ず誤り。
表より、SはPに負けたことが分かっている。
よって、ウ「Sは全勝だった」は必ず誤り。
Q12,総当たり2
P、Q、R、Sの4チームが、バスケットボールの試合を総当たり戦で行った。その試合結果について、次のことが分かっている。
- ⅰ)Pは2勝1敗だった
- ⅱ)PはQに勝った
- ⅲ)RはPに勝った
- ⅳ)SはQに勝った
- ⅴ)引き分けの試合は無かった
- (2)更にどのような情報が追加されれば、全ての試合の勝敗が決まるか。ただし、情報として追加する選択肢は、できる限り抑えるものとする。
- カQは1勝2敗だった
- キRは1勝2敗だった
- クSは2勝1敗だった
(1)でまとめた表を元に、追加される情報カ~クについて考える。
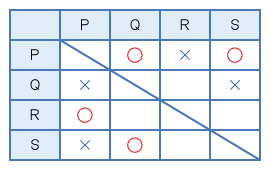
表より、カ「Qは1勝2敗だった」からは、QがRに勝ったことが新たに分かるが、R対Sの結果は分からない。
表より、キ「Rは1勝2敗だった」からは、RがQ、S両方に負けたことが新たに分かるため、全ての試合の勝敗が決まる。
表より、ク「Sは2勝1敗だった」からは、SがRに勝ったことが新たに分かるが、Q対Rの結果は分からない。
したがって、キだけ追加されれば、全ての試合の勝敗が決まる。
Q13、トーナメント
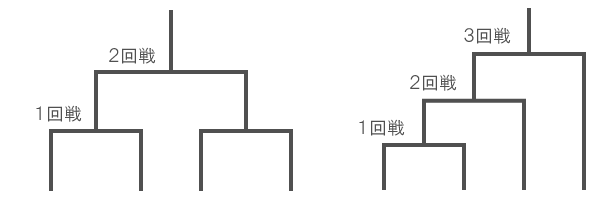
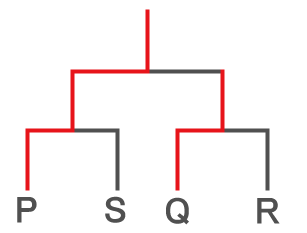
P、Q、R、Sの4人でテニスのトーナメント戦をすることになった。その結果として、以下のことが分かっている。
- ⅰ)PはQに勝った
- ⅱ)RはQに負けた
ただし、トーナメント形式が上2つのどちらであったかは分からない。
(1) 次のア、イの正誤を考え、AからIまでの中から正しいものを1つ選びなさい。
- ア)Pは2回戦を戦っている
- イ)Sは1回しか戦っていない
与えられた情報を整理する。
3回戦がないトーナメント形式の場合は以下のパターンのみ。
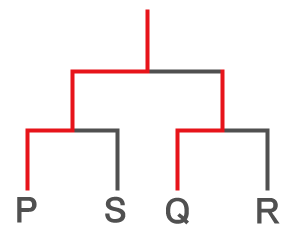
3回戦のあるトーナメント形式の場合は以下の4つのパターンがある。
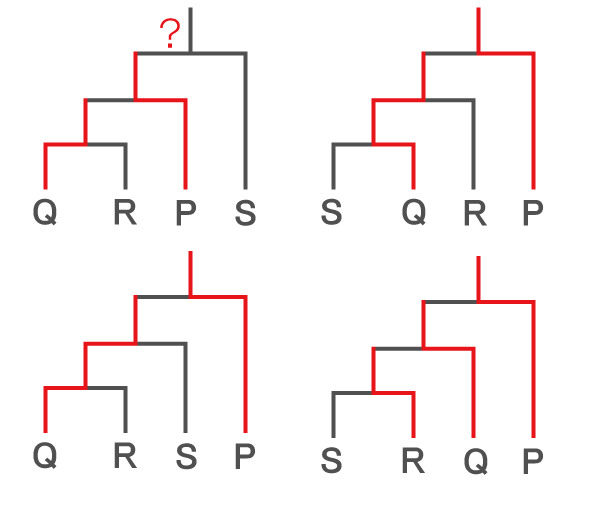
ア)Pは2回戦を戦っている → わからない。
上図にて、Pが2回戦を戦っているものと戦っていないものがあるため、わからない。
QとRの対戦でQが勝った後にPとQが当たるんだから、2回戦で戦うはず!と決めつけないように!
それよりも前にSがQとRのいずれかと戦うパターンを忘れずに。
イ)Sは1回しか戦っていない → 正しい。
どちらのトーナメント形式の場合も、総試合数は3回。
2つの試合は、PとQ、QとRとの対戦だったのだから、残りの1試合だけがSが出場した試合とわかる。
Q14、トーナメント2
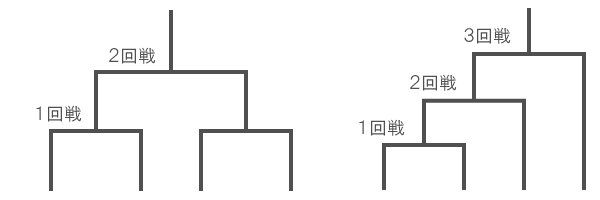
P、Q、R、Sの4人でテニスのトーナメント戦をすることになった。その結果として、以下のことが分かっている。
- ⅰ)PはQに勝った
- ⅱ)RはQに負けた
ただし、トーナメント形式が上2つのどちらであったかは分からない。
(2) 次の情報のうち、どちらが追加されたらトーナメント表と試合結果が確定するか。
- ア)Sが優勝した
- イ)PはQと2回戦で戦った
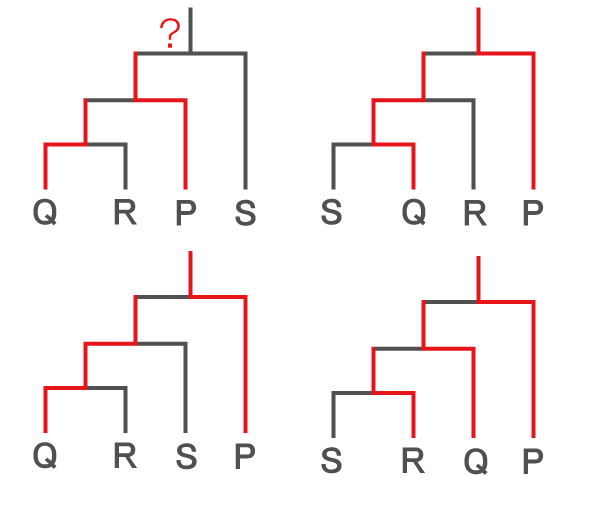
ア)Sが優勝した
だけが分かっていた場合 → 確定する。
Sが優勝するのは、3回戦で初めて戦う位置にSがおり、かつ、3回戦でPに勝つパターンのみ。
イ)PはQと2回戦で戦った
だけが分かっていた場合 → 確定しない。
PがQと2回戦で戦うパターンは上図のうち2つ存在する。
Q15、位置関係

上図のような2階建てのアパートに、P、Q、R、S、T、Uの6人が1人1部屋で住んでいて、次のことが分かっている。
- ⅰ)Pは201号室に住んでいる
- ⅱ)Qの真下にはTが住んでいる
- ⅲ)Rの隣のうち、一方には誰かが住んでいて、もう一方は空き室である
- ⅳ)Sの右隣にはUが住んでいる
- ⅴ)Uは端には住んでいない
- (1)次のア、イの正誤を考え、AからIまでの中から正しいものを1つ選びなさい。
- アPの真下は空き室である
- イSの左隣にはTが住んでいる
位置関係を推論する問題は、与えられた情報から、想定できる位置関係のパターンを全て洗い出す。
まず・・・
ⅰ)「Pは201号室に住んでいる」
ⅳ)「Sの右隣にはUが住んでいる」
ⅴ)「Uは端には住んでいない」
ということから、P、S、Uについて、1-a~1-cの3パターンが考えられる。

次に・・・
ⅱ)「Qの真下にはTが住んでいる」
ということから、QとTを加えて、1-aから1パターン(2-a)、1-bから2パターン(2-b、2-c)、1-cから1パターン(2-d)、計4パターンが考えられる。

最後に・・・
ⅲ)「Rの隣のうち、一方には誰かが住んでいて、もう一方は空き室である」
ということから、Rと空き室を加えて、2-aから1パターン(3-a)、2-cから2パターン(3-b、3-c)、2-dから2パターン(3-d、3-e)、計5パターンが考えられる。

3-a~3-eをもとに、推論ア、イについて考えていこう。
アPの下は空き室である → 分からない。
3-a、3-d、3-eではPの真下が空き室だが、3-b、3-cではPの真下がSである。
よって、ア「真下は空き室である」は分からない。
イSの左隣にはTが住んでいる → 誤り。
3-a~3-eのいずれも、Sの左隣はTではない。
よって、ア「Sの左隣にはTが住んでいる」は誤り。
Q16、位置関係2

上図のような2階建てのアパートに、P、Q、R、S、T、Uの6人が1人1部屋で住んでいて、次のことが分かっている。
- ⅰ)Pは201号室に住んでいる
- ⅱ)Qの真下にはTが住んでいる
- ⅲ)Rの隣のうち、一方には誰かが住んでいて、もう一方は空き室である
- ⅳ)Sの右隣にはUが住んでいる
- ⅴ)Uは端には住んでいない
- (2)ⅰ)~ⅴ)に、「ⅵ) Uの上は空き室である」という情報が加わった。 このとき、次のカ、キ、クの推論のうち、必ず正しいものはどれか。
- カPの右隣にはRが住んでいる
- キUの右隣にはTが住んでいる
- ク空き室は1階と2階に1部屋ずつある
新しい情報である、ⅵ)「Uの上は空き室である」を3-a~3-eに当てはめると、部屋の割り当ては3-cか3-dであると分かる。
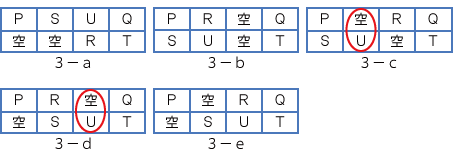
3-c、3-dをもとに、推論カ、キ、クについて考えていこう。
Pの右隣は、3-dではRが住んでいるが、3-cでは空き室である。よって、カ「Pの右隣にはRが住んでいる」は正しいとは限らない。
Uの右隣は、3-dではTが住んでいるが、3-cでは空き室である。よって、キ「Uの右隣にはTが住んでいる」は正しいとは限らない。
3-cと3-dのいずれも、空き室は1階と2階に1部屋ずつある。よって、ク「空き室は1階と2階に1部屋ずつある」は必ず正しい。
Q17、位置関係(複数回答)

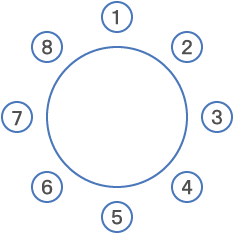
図のようなテーブル席に、P、Q、R、Sの4人が座る。4人の座った場所について、以下のことが分かっている。
- ⅰ)Pは1に座る。
- ⅱ)Qの真正面にはRが座っている。
(1)SがQの左隣りに座っている場合、Sが座っている可能性があるのはどの席か。当てはまるものをすべて選びなさい。
「左隣り」とは、例えばQが1に座っている場合、その左隣りは2を指す。
条件に当てはまる4人の座り方は数えるほどしかないので、全てのパターンを考えればOK!
既に1に座っているPとかぶらないように、Q、R、Sを当てはめていけば、以下の5通りがあると分かる。
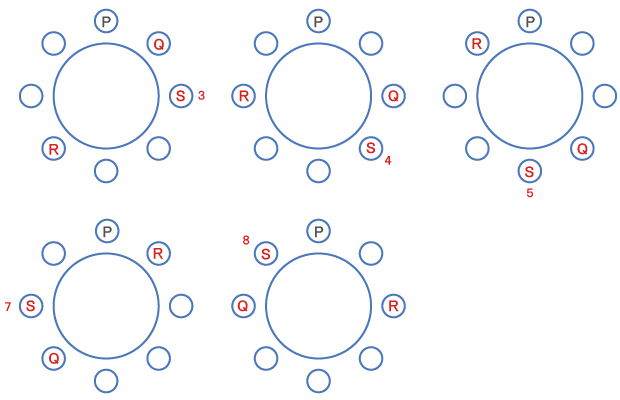
Q18、位置関係(複数回答)2
図のようなテーブル席に、P、Q、R、Sの4人が座る。4人の座った場所について、以下のことが分かっている。
- ⅰPは1に座る。
- ⅱQの真正面にはRが座っている。
(2)Sの両隣りに誰も座っていないとき、Sが座った可能性があるのはどの席か。当てはまるものをすべて選びなさい。
A→4 , E5 , F6
(1)同様、条件に当てはまる4人の座り方は数えるほどしかないので、全てのパターンを考えればOK!
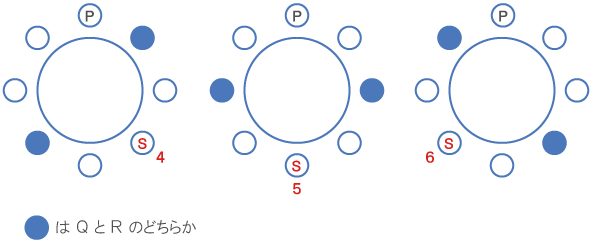
以上より、Sが座る可能性があるのは4、5、6。
Q19、条件
以下について、ア、イの情報のうち、どちらがあれば[設問]の答えが定まるか。AからEの中から正しいものを1つ選びなさい。
[設問]
サイコロ2つを同時に振ったところ、出た目の差は2であった。出た目はそれぞれいくつであったか。
- ア「2つのサイコロの積」の約数の数は4つであった。
- イ「2つのサイコロの和」の約数の数は4つであった。
提示された2つの条件のうちどちらが必要かを推論する問題は、まず片方の条件だけで成立するかを考え、成立しなければ2つの条件で成立するか考える。
「出た目の差が2であった」ことから、考えられるパターンは・・・
[1,3]、[2,4]、[3,5]、[4,6]
の4つである。
ア「2つのサイコロの積」の約数の数は4つであった。
が分かっていた場合、
[1,3]・・・積は31。約数の数は2個(30 → 1、31 → 3)。
[2,4]・・・積は23。約数の数は4個(20 → 1、21 → 2、22 → 4、23 → 8)
[3,5]・・・積は31×51。約数の数は、(1 + 1)×(1 + 1)= 4個
[4,6]・・・積は23×31。約数の数は、(3 + 1)×(1 + 1)= 8個
よって、[2,4]と[3,5]のパターンが考えられる。アだけでは1つに定まらない。
イ「2つのサイコロの和」の約数の数は4つであった。
が分かっていた場合、
[1,3]・・・和は4 = 22。約数の数は3個
[2,4]・・・和は6 = 21×31。約数の数は、(1 + 1)×(1 + 1)= 4個
[3,5]・・・和は8 = 23。約数の数は4個
[4,6]・・・和は10 = 21×51。約数の数は、(1 + 1)×(1 + 1)= 4個
よって、[2,4]と[3,5]と[4,6]のパターンが考えられる。イだけでも1つに定まらない。
アとイ両方が分かっていたとしても、[2,4]、[3,5]のパターンが考えられるため、1つに定まらない。
よって、アとイ両方あってもわからない ⇒ Eが正解。
Q20、条件2
以下について、ア、イの情報のうち、どちらがあれば[設問]の答えが定まるか。AからEの中から正しいものを1つ選びなさい。
[設問]
ある商品の値段を通販サイトP、Q、Rで比較したところ、PはQより500円安く販売しており、3社とも6500円以上で販売していることが分かった。
PはRよりも何円安く、または高くこの商品を販売しているか。
- アいずれかの通販サイトでは6900円で販売している。
- イ平均は6800円であった。
「PはRよりも何円安く、または高くこの商品を販売しているか」という設問だが、これだと分かりにくいので、
「P、Q、Rがそれぞれ何円でこの商品を販売しているか」
が分かるか、で考えていけば良い。
「P、Rの価格差が分かっているがそれぞれがいくらかは分からない」ということは条件によってはありうるが、 今回は具体的な値段が書かれているため問題ない。
アいずれからの通販サイトでは6900円で販売している。
だけが分かっていた場合 ⇒ 特定できない。
P、Qのいずれかが6900円であれば、「PはQより500円安く販売して」いることから、P、Qの値段は分かるが、
(正確には「3社とも6500円以上」から[P,Q] = [6400,6900]のパターンはない)
Rについては「6500円以上」以外の情報がないため、特定できない。
Rが6900円だとしても、P、Qの値段の特定まではできない。
イ平均は6800円であった。
だけが分かっていた場合 ⇒ 特定できない。
方程式で考えれば、
P – Q = -500
P + Q + R = 6800 × 3
と2つの式が分かっているが、変数が3つの方程式の解を求めるためには3つの式が必要なため、1つ式が不足している状態である。
アとイの両方が分かっていた場合 ⇒ 特定できる。
Qが6900円のケースは、Pが6400円になって、「3社とも6500円以上」に反してしまうので、
Pが6900円のケース、Rが6900円のケースについて考える。
Pが6900円の場合、Qは7400円である。平均が6800なので、Rは
6800 × 3 – 6900 – 7400 = 6100円
となるが、これは「3社とも6500円以上」に反する。
Rが6900円の場合、P、Qの値段の合計は
6800 × 3 – 6900 = 13500円
これは、P + Q = 13500 と言い換えられる。
これと、P – Q = -500 より、
P = 6500円、Q = 7000円となる。これは「3社とも6500円以上」を満たしている。
よって、P、Q、Rの値段が1つに定まったため、
ア、イ両方が分かれば答えが定まる ⇒ Cが正解。
