確率について

＜ポイント＞

[ Aが起こる確率 ] = [ Aが起こる場合の数 ] / [ 全ての場合の数 ]
・・・ということなので、場合の数がキチンと理解できていれば、超カンタンです！

  • [ Aが起こる確率 ] = [ Aが起こる場合の数 ] / [ 全ての場合の数 ]・・・基本問題1
  • 「AまたはBの確率」→ 2つの確率を足し合わせよう！ → 和の法則・・・基本問題2
  • 「AかつBの確率」→ 2つの確率を掛け合わせよう！ → 積の法則・・・基本問題2
  • 「少なくとも・・・」→「問題文と反対の条件の確率」を考え、「1」（全体）から引こう！・・・基本問題2

※ 確率を勉強する前に

確率は分母も分子も「場合の数」ですから、場合の数を理解しておけばカンタン！
苦手な方はこちらから場合の数

 

 

 

＜基本問題＞

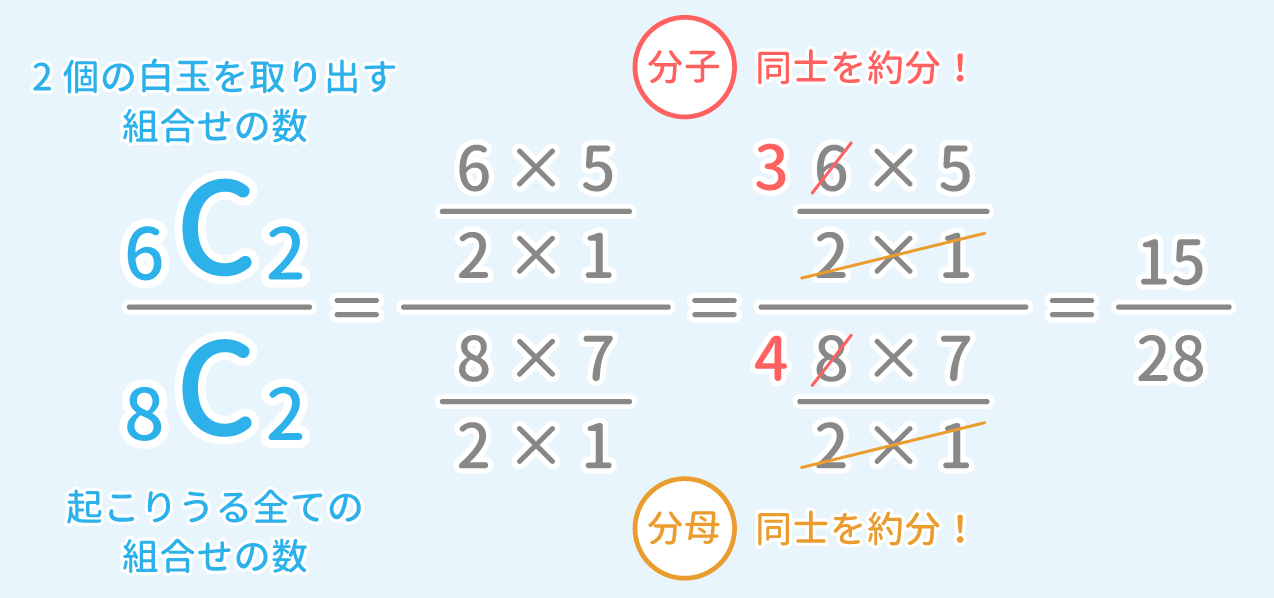
１、箱の中に赤玉が2個、白玉が6個入っている。この中から同時に2個の玉を取り出すとき、白玉を2個取り出す確率はいくらか。

Ａ→15 / 28

「確率」例題1 図1 Copyright （C） - SPI無料学習サイト（SPI3対応）【Study Pro】

2個の白玉を取り出す組合せの数は6C2である。
また、起こりうる全ての組合せの数は8C2である。
したがって、白玉を2個取り出す確率は

「確率」例題1 図2 Copyright （C） - SPI無料学習サイト（SPI3対応）【Study Pro】
———————————————————————————-

２、箱の中に青玉が1個、黄玉が2個、赤玉が3個入っている。

（1）玉を2個同時に取り出すとき、それらが同色の玉である確率はいくらか。

（2）玉を1個取り出し、色を確認して箱の中に戻し、再び玉を1個取り出す。このとき、どちらも赤玉である確率はいくらか。

（3）玉を1個取り出し、色を確認して箱の中に戻し、再び玉を1個取り出す。このとき、少なくとも1個は青玉である確率はいくらか。

 

 

  • Ａ→（1）　B．4 / 15
  • 「同色の玉」には、「2個とも黄玉」と「2個とも赤玉」という2パターンが考えられる。
  • 2個とも黄玉である確率は
  • 式）2C2 / 6C2 = {（2×1） / （2×1）} / {（6×5） / （2×1）} = 1 / 15
  • 2個とも赤玉である確率は
  • 式）3C2 / 6C2 = {（3×2） / （2×1）} / {（6×5） / （2×1）} = 1 / 5
  • 「2個とも黄玉」または「2個とも赤玉」の確率を求めればよいので、それぞれの確率を足し合わせる。
  • 式）（1 / 15） + （1 / 5） = 4 / 15
  • 「AまたはBの確率」ときたら、「2つの確率を足し合わせる」と覚えておこう。→ 和の法則
  • Ａ→（2）　F．1 / 4
  • 1回目が赤玉である確率は「3 / 6」なので、約分すると「1 / 2」である。
    また、2回目が赤玉である確率も同様に「1 / 2」である。
  • 「1回目が赤玉」かつ「2回目も赤玉」の確率を求めればよいので、それぞれの確率を掛け合わせる。
  • 式）（1 / 2）×（1 / 2） = 1 / 4
  • 「AかつBの確率」ときたら、「2つの確率を掛け合わせる」と覚えておこう。 → 積の法則
  • Ａ→（3）　G．11 / 36
  • 「少なくとも・・・」ときたら、「問題文と反対の条件の確率」を考え、「1」（全体）から引く。
  • 問題の条件である「少なくとも1個は青玉である」の反対は「2回とも青玉ではない」
    言い換えると「2回とも黄玉か赤玉」である。
  • 2回とも黄玉か赤玉の確率は
  • 式）（5 / 6）×（5 / 6） = 25 / 36
  • したがって、少なくとも1個は青玉である確率は
  • 式）1 – [ 2回とも黄玉か赤玉である確率 ]
    = 1 – （25 / 36）
    = 11 / 36

 

 

 

Ｑ１、組み合わせ

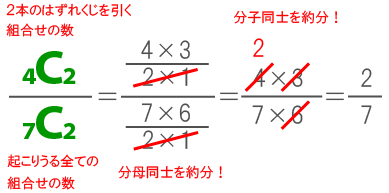
箱の中に、3本の当たりくじと4本のはずれくじが入っている。このくじを2本同時に引く。

（1）2本ともはずれくじを引く確率はいくらか。

 

Ａ→2 / 7

2本のはずれくじを引く組合せの数は、4C2である。
起こりうる全ての組合せの数は、7C2である。

したがって、2本ともはずれくじを引く確率は

 

 

Ｑ２，組み合わせ02

箱の中に、3本の当たりくじと4本のはずれくじが入っている。このくじを2本同時に引く。

（2）当たりくじとはずれくじを1本ずつ引く確率はいくらか。

 

Ａ→4 / 7

当たりくじとはずれくじを1本ずつ引く組合せの数は、（4×3）通りである。
起こりうる全ての組合せは、7C2である。

求める確率は

  1. 式）（4×3） / 7C2 = （4×3） / {（7×6） / （2×1）} = 4 / 7

 

 

Ｑ３，積の法則

信号P、Qを車で通過する。信号Pを青で通過できる確率は0.7、信号Qを青で通過できる確率は0.4である。

（1）信号Pも信号Qも青で通過できる確率はいくらか。

Ａ→0.28

「信号Pが青」かつ「信号Qが青」の確率を求めればよいので、それぞれの確率を掛け合わせる。

  1. 式）0.7×0.4 = 0.28

「AかつBの確率」ときたら、「2つの確率を掛け合わせる」と覚えておこう。 → 積の法則

 

 

Ｑ４、和の法則

信号P、Qを車で通過する。信号Pを青で通過できる確率は0.7、信号Qを青で通過できる確率は0.4である。

（2）どちらか一方の信号だけ青で通過できる確率はいくらか。

 

Ａ→0.54

「どちらか一方の信号だけ青」には、「信号Pだけ青」と「信号Qだけ青」という2パターンが考えられる。

青の確率は問題文に書かれているので、青でない確率を求めておこう。
信号Pが青の確率は「0.7」 → 信号Pが青でない確率は「0.3」
信号Qが青の確率は「0.4」 → 信号Qが青でない確率は「0.6」

信号Pだけ青の確率は

  1. 式）0.7×0.6 = 0.42

信号Qだけ青の確率は

  1. 式）0.3×0.4 = 0.12

「信号Pだけ青」または「信号Qだけ青」の確率を求めればよいので、それぞれの確率を足し合わせる。

  1. 式）0.42 + 0.12 = 0.54

「AまたはBの確率」ときたら、「2つの確率を足し合わせる」と覚えておこう。→ 和の法則

なお、全てのパターンを表にすると次のようになる。
全ての確率を足し合わせると「1」（0.28 + 0.42 + 0.12 + 0.18）になるため、時間に余裕がある場合は、計算ミスがないか確認しよう。

信号Q
青（0.4） 青以外（0.6）
信号P 青（0.7） 0.28 0.42
青以外（0.3） 0.12 0.18

 

 

Ｑ５，くじを戻す場合と戻さない場合

8本中、4本が当たりのくじがある。このくじを3回続けて引く。

（1）一度引いたくじはもとに戻さないものとする。このとき、3本とも当たりくじを引く確率はいくらか。

 

Ａ→1 / 14

1回目に当たりくじを引く確率は「4 / 8」。
当たりくじが1本なくなっているため、2回目に当たりくじを引く確率は「3 / 7」。
当たりくじが2本なくなっているため、3回目に当たりくじを引く確率は「2 / 6」。

「1回目当たり」かつ「2回目当たり」かつ「3回目当たり」の確率を求めればよいので、それぞれの確率を掛け合わせる。

  1. 式）（4 / 8）×（3 / 7）×（2 / 6） = 1 / 14

 

 

Ｑ6．くじを戻す場合と戻さない場合

8本中、4本が当たりのくじがある。このくじを3回続けて引く。

（2）くじを引いたとき、はずれくじの場合は元に戻し、当たりくじの場合は元に戻さないものとする。 このとき、当たりくじ、はずれくじ、当たりくじの順で引く確率はいくらか。

 

Ａ→6 / 49

1回目に当たりくじを引く確率は「4 / 8」。
当たりくじが1本なくなっているため、2回目にはずれくじを引く確率は「4 / 7」。
当たりくじが1本なくなっているため、3回目に当たりくじを引く確率は「3 / 7」。

「1回目当たり」かつ「2回目はずれ」かつ「3回目当たり」の確率を求めればよいので、それぞれの確率を掛け合わせる。

  1. 式）（4 / 8）×（4 / 7）×（3 / 7） = 6 / 49

 

 

Ｑ7．少なくとも＜余事象＞

スペードの1から13まで、合計13枚のトランプの山がある。この山からトランプを2枚続けて引く。

（1）1枚目に引いたカードを山に戻して、よく切った後に2枚目のカードを引く。このとき、少なくとも1枚は3の倍数である確率はいくらか。

Ａ→88 / 169
  • 『少なくとも・・・』ときたら、「問題文と反対の条件の確率」を考え、「1」（全体）から引く。
  • 問題の条件である「少なくとも1枚は3の倍数」の反対は、「2枚とも3の倍数以外」である。
  • 1枚目に3の倍数（3、6、9、12）以外を引く確率は「9 / 13」。
    1枚目に引いたカードを山に戻してから、2枚目のカードを引くので、2枚目に3の倍数以外を引く確率も「9 / 13」。
  • よって、2枚とも3の倍数以外である確率は
  1. 式）（9 / 13）×（9 / 13） = 81 / 169
  • したがって、少なくとも1枚は3の倍数である確率は
  1. 式）1 – [ 2枚とも3の倍数以外である確率 ]
    = 1 – 81 / 169
    = 88 / 169

 

 

Ｑ８、少なくとも＜余事象＞2

スペードの1から13まで、合計13枚のトランプの山がある。この山からトランプを2枚続けて引く。

（2）1枚目に引いたカードを山に戻さず、2枚目のカードを引く。このとき、少なくとも1枚は5の倍数である確率はいくらか。

A→23 / 78
  • 問題の条件である「少なくとも1枚は5の倍数」の反対は、「2枚とも5の倍数以外」である。
  • 1枚目に5の倍数（5,10）以外を引く確率は「11 / 13」。
    5の倍数以外が1枚減っているため、2枚目に5の倍数以外を引く確率は「10 / 12」。
  • よって、2枚とも5の倍数以外である確率は
  • 式）（11 / 13）×（10 / 12） = 55 / 78
  • したがって、少なくとも1枚は5の倍数である確率は
  • 式）1 – [ 2枚とも5の倍数以外である確率 ]
    = 1 – 55 / 78
    = 23 / 78

 

 

Ｑ９，サイコロの目

大小2つのサイコロを同時に投げる。

（2）2つのサイコロの目の積が偶数になる確率はいくらか。

 

Ａ→3 / 4

大小のサイコロの積のパターンをまとめると下表のようになる。

[ 大小のサイコロの積のパターン ]
小
偶数 奇数
大 偶数 積は偶数 積は偶数
奇数 積は偶数 積は奇数

2つのサイコロの目の積が偶数になるのは、黄色マス（青字）の3パターンである。
したがって、[大,小] = [偶数,偶数]、[偶数,奇数]、[奇数,偶数]の全てのパターンの確率を求めて、足し合わせればよい。

  1. 式）（3 / 6）×（3 / 6） + （3 / 6）×（3 / 6） + （3 / 6）×（3 / 6）
    = 1 / 4 + 1 / 4 + 1 / 4
    = 3 / 4

 

Ｑ10、サイコロの目2

大小2つのサイコロを同時に投げる。

（2）2つのサイコロの目の和が10以上になる確率はいくらか。

大小のサイコロの和のパターンをまとめると下表のようになる。

[ 大小のサイコロの和のパターン ]
小
1 2 3 4 5 6
大 1 2 3 4 5 6 7
2 3 4 5 6 7 8
3 4 5 6 7 8 9
4 5 6 7 8 9 10
5 6 7 8 9 10 11
6 7 8 9 10 11 12

2つのサイコロの目の和が10以上となるのは、表中の黄色マス（青字）なので、6通りが考えられる。
一方、起こりうる全ての場合の数は（6×6）通り。
したがって、求める確率は

  1. 式）6 / （6×6） = 1 / 6

 

 

Ｑ11，積の法則

箱の中に、赤玉が3個、黄玉が2個、青玉が1個入っている。
箱の中から玉を1個取り出し、色を確認した後、箱に戻す。これを3回繰り返す。

（1）1回目に赤玉、2回目に黄玉、3回目に青玉を取り出す確率はいくらか。

Ａ→1 / 36

1回目に赤玉を取り出す確率は、3 / 6。
2回目に黄玉を取り出す確率は、2 / 6。
3回目に青玉を取り出す確率は、1 / 6。

「1回目に赤玉」かつ「2回目に黄玉」かつ「3回目に青玉」の確率を求めればよいので、それぞれの確率を掛け合わせる。

  1. 式）（3 / 6）×（2 / 6）×（1 / 6） = 1 / 36

 

 

Ｑ12、場合分け

箱の中に、赤玉が3個、黄玉が2個、青玉が1個入っている。
箱の中から玉を1個取り出し、色を確認した後、箱に戻す。これを3回繰り返す。

（2）3回目に2個目の青玉を取り出す確率はいくらか。

Ａ→5 / 108

3回目に2個目の青玉を取り出すパターンは以下の2パターンが考えられる。

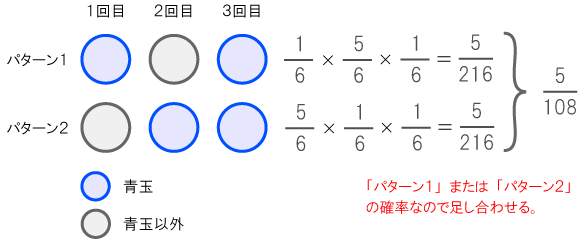
よって、求める確率は、5 / 108である。