<ポイント>
「ある割合の中の、更にある割合」を求める問題です。
表の読み取りでもよく出題されますね(*´∀`*)
図をイメージすると計算式が導きやすくなります!苦手な人は是非お試しを!
- 「割合×割合」の使い方を押さえよう!
- 苦手な人は図をイメージしよう!
【割合×割合】
ある割合の中の、更にある割合を求める場合は、割合を掛け合わせます。
例えば、対象全体の中の高校生の割合が40%で、高校生の中の男子の割合が60%のとき、対象全体から見たときの高校生の男子の割合は、次のように24%となります。
- 式)0.40×0.60 = 0.24 → 24(%)
【割合の単位】
割合を表す単位には、「割」「%」が使われます。
計算をする前に小数に変換しましょう。
「1割」 → 「0.1」(1 / 10すればOK)
「25%」 → 「0.25」(1 / 100すればOK)
【内項の積、外項の積】・・・問題3-1
a : b = c : d
のとき、
(外項)a×d = b×c(内項)
が成り立ちます。考えてみれば当たり前な公式ですね(ノ∀`;)
例えば・・・
2 : 3 = 6 : xなら、
2x = 3×6 = 18
x = 9 となります。
![]()
<基礎問題>
Q,ある大学の研究室には3000冊の書籍が保管されている。このうち30%は法律書である。
(1)法律書以外の書籍のうち、20%が経済書であった。経済書は何冊か。
- A180冊
- B240冊
- C300冊
- D360冊
- E420冊
- F540冊
- G600冊
- H660冊
(2)100冊の法律書を外部に譲渡した場合、残った法律書は研究室の書籍全体の何%となるか(必要なときは、最後に小数点以下第1位を四捨五入すること)。
- A25%
- B26%
- C27%
- D28%
- E29%
- F30%
- G31%
- H32%
↓ 回答
問題文の情報を図にまとめると次のようになる。
「?」の部分を求めればよい。
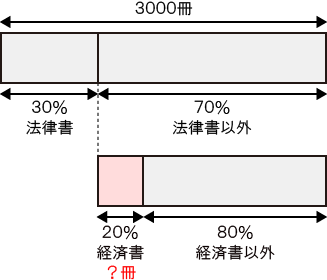
ある割合の中の、更にある割合を求める場合は、割合を掛け合わせる。
- 式)3000×0.70×0.20 = 420(冊)
100冊の法律書を譲渡したので、残った法律書は、
- 式)3000×0.30 – 100 = 800(冊)
また、研究室の書籍全体も100冊減らすことに注意しよう。
- 式)3000 – 100 = 2900(冊)
したがって、求める割合は、
- 式)800÷2900 = 0.275・・・ → 27.5・・・(%)
小数点以下第1位を四捨五入するので、28%が答えとなる。
![]()
Q1、(割合×割合)
ある日の国立博物館Pの訪問者数は8000人で、そのうち40%が女性の訪問者であった。
(1)男性の訪問者のうち、70%が20歳以上であった。20歳未満の訪問者は何人か。
問題文の情報を図にまとめると次のようになる。
「?」の部分を求めればよい。
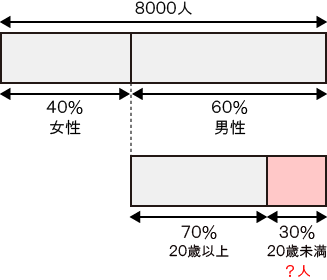
ある割合の中の、更にある割合を求める場合は、割合を掛け合わせる。
- 式)8000×0.60×0.30 = 1440(人)
Q2、(一部の数が増加する)
ある日の国立博物館Pの訪問者数は8000人で、そのうち40%が女性の訪問者であった。
(2)男性の訪問者は変わらず、女性の訪問者だけが1000人増えた場合、女性の訪問者は全体の何%となるか(必要なときは、最後に小数点以下第1位を四捨五入すること)。
A,→47%
女性の訪問者だけが1000人増えたので、女性の訪問者数は、
- 式)8000×0.40 + 1000 = 4200(人)
また、訪問者数全体も1000人増やすことに注意しよう。
- 式)8000 + 1000 = 9000(人)
したがって、求める割合は、
- 式)4200÷9000 = 0.466・・・ → 46.6・・・(%)
小数点以下第1位を四捨五入するので、47%が答えとなる。
Q3,(割合×割合)
イチゴ、抹茶、黒チョコ、白チョコの4種類のクッキーと平らな箱がある。 箱全体の20%の面積にイチゴクッキーを敷きつめた。
(1)イチゴクッキーを敷きつめた面積の3 / 4倍の面積に抹茶クッキーを敷きつめ、残りの面積には黒チョコクッキーを敷きつめたとき、黒チョコクッキーの面積は箱全体の何%か。
A、65%
問題文の情報を図にまとめると次のようになる。
「?」の部分を求めればよい。
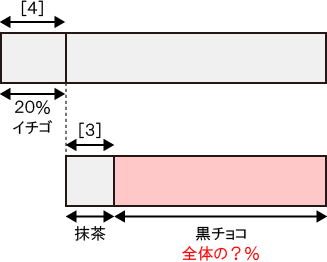
まず、抹茶クッキーの面積が全体の何%かを求める。
- 式)0.20×(3 / 4) = 0.15 → 15(%)
残りの面積は黒チョコクッキーなので、
- 式)1 – 0.20 – 0.15 = 0.65 → 65(%)
Q4、(小数と比)
イチゴ、抹茶、黒チョコ、白チョコの4種類のクッキーと平らな箱がある。 箱全体の20%の面積にイチゴクッキーを敷きつめた。
(2)残った面積の30%に抹茶クッキーを敷きつめ、更に残った面積には黒チョコクッキーと白チョコクッキーを2:3の割合で敷きつめたとき、 黒チョコクッキーの面積は箱全体の何%か(必要なときは、最後に小数点以下第1位を四捨五入すること)。
A、22%
問題文の情報を図にまとめると次のようになる。
「?」の部分を求めればよい。
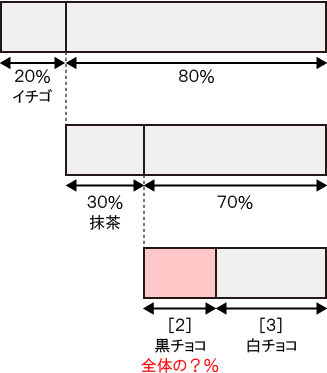
- 式)0.80×0.70×(2 / 5) = 0.224 → 22.4(%)
小数点以下第1位を四捨五入するので、22%が答えとなる。
Q5,(2つの割合)
箱Pにはミカン、リンゴ、イチゴの個数がそれぞれ30%、50%、20%の割合で入っており、箱Qにはそれぞれ20%、40%、40%の割合で入っている。箱Qに入っている果物をすべて箱Pに移した。
(1)箱Qの果物を箱Pに移した後、リンゴとイチゴの数の比が4:3になった。箱Qに入っていた果物の数は、箱Qの中身を移す前の箱Pの何倍か。
A、(7 / 4)倍
具体的な数が与えられていないので、Pの果物の総数を100個とおいて計算する。
Qに入っている果物の数をPのx倍とすれば、Qに入っている果物の数は100x(個)。
箱Pに移した後のリンゴの数は、(50 + 40x)個。
イチゴの数は、(20 + 40x)個。
リンゴとイチゴの比が4:3だから、
(50 + 40x):(20 + 40x)= 4 : 3
内項の積と外項の積が等しいので、
3×(50 + 40x) = 4×(20 + 40x)
40x = 70
x = 7/4(倍)
Q6,(2つの割合)
箱Pにはミカン、リンゴ、イチゴの個数がそれぞれ30%、50%、20%の割合で入っており、箱Qにはそれぞれ20%、40%、40%の割合で入っている。箱Qに入っている果物をすべて箱Pに移した。
(2)箱Qの果物を箱Pに移した後、Pからミカンを4個取り出したところ、ミカンとイチゴの数の比が1:2になった。箱Qに入っていた果物の数はいくつか。
A、35個
(1)より、箱Qの果物の数は箱Pの(7 / 4)倍なので、
Pに入っていたミカン、リンゴ、イチゴの個数をそれぞれ[ 30 ]、[ 50 ]、[ 20 ]と表すと、
Qのミカンは、[ 20 ] ×(7 / 4)= [ 35 ]
リンゴは、[ 40 ] ×(7 / 4)= [ 70 ]
イチゴは、[ 40 ] ×(7 / 4)= [ 70 ]
これを表にすると以下のようになる。
| ミカン | リンゴ | イチゴ | 合計 | |
| 箱P | [ 30 ] | [ 50 ] | [ 20 ] | [ 100 ] |
| 箱Q | [ 35 ] | [ 70 ] | [ 70 ] | [ 175 ] |
| 合計 | [ 65 ] | [ 120 ] | [ 90 ] | [ 275 ] |
ミカンを4個取り出すと、ミカンとイチゴの数の比が1:2になるのだから、
([ 65 ] – 4): [ 90 ] = 1 : 2
内項、外項の積が等しいので、
2 ×([ 65 ] – 4)= [ 90 ]
[ 40 ] = 8
[ 1 ] = 1 / 5(個)
Qに入っていた果物の数は、[ 175 ] 個なので、 (1 / 5)×175 = 35(個)
