<ポイント>
- 「一人当たりの支払い平均額」を求めよう!・・・例題1、例題2
- 貸し借りがある場合は「それぞれの借金のプラス / マイナス」を整理しよう!・・・問題4
3人、4人がそれぞれお金を出して商品を買って、最終的に「割り勘」に持っていく問題です。
それぞれにお金の貸し借りがある場合も(ノ∀`;)
ポイント1:「一人当たりの支払い額」を出すこと
例えば、3人がそれぞれ2000円、3000円、7000円の商品を買った場合、「一人当たりの支払い額」は4000円!
ポイント2:お金の貸し借りがある場合は、「それぞれの借金のプラス / マイナス」を整理すること
例えば、PはQに3000円貸していて、Rから1000借りている場合、「Pはプラス2000円の状態」!
頭の中だけで考えると意味不明になるので、この手順を踏んで解きましょう!(*´∀`*)
<基本問題>
①友人を祝うパーティーを開くために、Pは2000円、Qは2700円、Rは3700円のプレゼントを買った。 3人がプレゼント代を同額ずつ負担するためには、PとQはRにいくらずつ支払えばよいか。
- APは800円、Qは100円支払う
- BPは900円、Qは100円支払う
- CPは1000円、Qは100円支払う
- DPは1100円、Qは100円支払う
- EPは800円、Qは300円支払う
- FPは900円、Qは300円支払う
- GPは1000円、Qは300円支払う
- HPは1100円、Qは300円支払う
まず、「全ての商品の代金」から「一人当たりの支払い平均額」を求める。
全員の支払い総額は、
- 式)2000 + 2700 + 3700 = 8400(円)
よって、一人当たりの支払い平均額は、
- 式)8400÷3 = 2800(円)
したがって、同額ずつ負担するためには、次の通り精算すればよい。
現在Pは2000円分支払っている。 → 更に800円支払う。
現在Qは2700円分支払っている。 → 更に100円支払う。
現在Rは3700円分支払っている。 → 900円受け取る。
②友人を祝うパーティーを開くために、Pは2700円、Qは3800円のプレゼントを買い、Rはケーキの代金を支払った。 3人が同額ずつ負担するために、PはQに500円、RはQに100円支払った。このとき、ケーキの代金はいくらか。
- A3100円
- B3200円
- C3300円
- D3400円
- E3500円
- F3600円
- G3700円
- H3800円
まず、「一部の商品の代金」と「精算額」から「一人当たりの支払い平均額」を求める。
Pが支払った金額は、
- 式)2700 + 500 = 3200(円)
であり、この時点で精算も済んでいるため、一人当たりの支払い平均額も3200円である。
よって、全員の支払い総額は9600円(3200×3)である。
したがって、ケーキの代金は、
- 式)9600 – 2700 – 3800 = 3100(円)
———————————————————–
Q1、それぞれの支払額
P、Q、R、Sの4人でビンゴゲームをする。 ビンゴの景品を用意するため、Pが2000円、Qが1300円、Rが1700円の景品を買ったが、Sは何も買わなかった。 4人が景品代を同額ずつ負担するためには、誰が誰にいくらずつ支払えばよいか。
A→SはPに750円、Qに50円、Rに450円支払う
- 「全ての商品の代金」から「一人当たりの支払い平均額」を求める。
- 全員の支払い総額は、
- 式)2000 + 1300 + 1700 = 5000(円)
- よって、一人当たりの支払い平均額は、
- 式)5000÷4 = 1250(円)
- したがって、同額ずつ負担するためには、次の通り精算すればよい。
- 現在Pは2000円分支払っている。 → 750円受け取る。
現在Qは1300円分支払っている。 → 50円受け取る。
現在Rは1700円分支払っている。 → 450円受け取る。
現在Sは負担していない。 → 1250円支払う。
Q2、それぞれの支払額
P、Q、Rの3人はキャンプに行くための買い物に出かけた。 Pは2300円分の食べ物の材料を、Qは3700円分の調理器具を、Rはテントを買った。 後日、3人が同額ずつ負担するために、Rに対し、Pは2000円支払い、Qも600円支払った。 このとき、テントの代金はいくらか。
A→6900円
- 「一部の商品の代金」と「精算額」から「一人当たりの支払い平均額」を求める。
- Pが支払った金額は、
- 式)2300 + 2000 = 4300(円)
- であり、この時点で精算も済んでいるため、一人当たりの支払い平均額も4300円である。
よって、全員の支払い総額は12900円(4300×3)である。
したがって、テントの代金は、 - 式)12900 – 2300 – 3700 = 6900(円)
Q3、借金がある場合
友人のコンサートを祝うため、PとQは花束を買うことにした。 Pが3000円をQに渡し、Qが5000円の花束を買った。 また、PはもともとQに4000円貸していた。 花束の代金は同額ずつ負担し、2人の間の貸し借りを全て精算するためには、どちらがどちらにいくら支払えばよいか。
A→QがPに4500円支払う
- 買ったのは5000円の花束なので、一人当たりの支払い平均額は、
- 式)5000÷2 = 2500(円)
- PはQに3000円と、もともと貸していた4000円の、計7000円を負担している。
一方、支払う必要があるのは花束の半額であるのは、2500円。 - したがって、2人の間の貸し借りを全て精算するためには、QはPに4500円(7000 – 2500)支払えばよい。
Q4、借金がある場合
PはQに3000円貸しており、QはRに4000円貸しており、RはPに5000円貸している。
この3人が一緒に映画を見に行った。
映画の代金を全員同額ずつ負担したいが、ひとまずRが全員分の6000円を立て替えた。
3人の間の貸し借りを全て精算するにあたり、次の2つの方法を考えた。
① PがRに( ア )円支払い、QがRに( イ )円支払う。
② PがQに( ウ )円支払い、QがRに( エ )円支払う。
ただし、ア、イ、ウ、エに当てはまるものは正の整数であるものとする。
A→ウ:4000円、エ:5000円
「② PがQに( ウ )円支払い、QがRに( エ )円支払う。」となっており、PからRへ直接支払うことができないので、 下図の通り、PからRへ支払う分はQを経由して支払う形をとる。
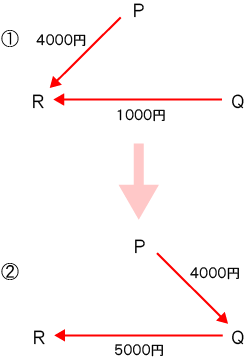
したがって、PがQに4000円支払い、QがRに5000円支払えばよい。
Q5、謝った精算
3兄弟のP、Q、Rは母の誕生日プレゼントにマフラーを買うことにした。 PはQから6000円を預かり、もともと7000円貸していたRからは12000円お金を預かって出かけた。 結局、Pは24000円のマフラーを買うことになった。
(1)この後、3人の貸し借りがすべてなくなるよう代金の精算をすることとなった。 Rは「僕はPから7000円借りていて、12000円を預けたから、差額の半分の2500円返してくれるかな」と言い、 Pは「Qからは追加で2000円もらえるかな。プレゼント代は一人あたり8000円だから、預かった額との差を考えれば、それで帳尻が合うはず」と言った。 このように精算するとPはいくら得、または損をするか。
A→5500円損をする
損得を計算するには、「貸し借りがなくなるように精算を行ったとき」「問題文通りに精算を行ったとき」と比較すればよい。
まず、貸し借りがなくなるように精算を行った場合、誰がいくら払うのか、整理する。

貸し借りがなくなるように精算を行うのであれば、以下のように精算を行えばよい。

問題文通りに精算を行った場合、以下のようになる。
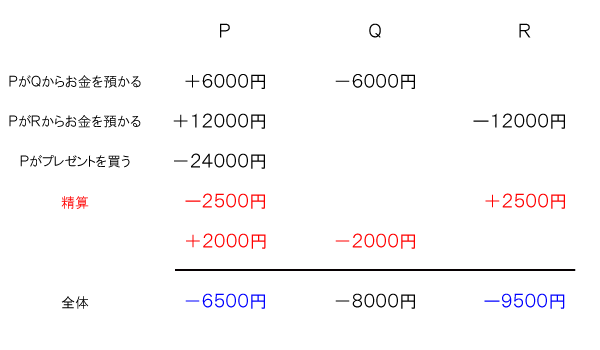
以上の2つを比べると、Pは
式)-6500 -(-1000)= -5500
→5500円損していることになる。
Rさん、自分から申し出て儲けようとしているあたりなかなかのごうつくばりですね・・・(ノ∀`;)
Q6、誤った計算2
3兄弟のP、Q、Rは母の誕生日プレゼントにマフラーを買うことにした。 PはQから6000円を預かり、もともと7000円貸していたRからは12000円お金を預かって出かけた。 結局、Pは24000円のマフラーを買うことになった。
(2)3人の貸し借りがすべてなくなるような正しい精算の仕方は次のうちどれか。
(1)で示した正しい精算方法に合う選択肢を選べばOK。

「QがPに2000円支払い、RがPに3000円を支払う」が正解。
