<ポイント>
「命題」って覚えてますか?(ノ∀`;)
頭の中だけで考えると混乱してしまいますが、 「対偶」と「三段論法」を使うと、それぞれの関連性をカンタンに把握できます!(*´∀`*)
【逆】
命題 [ Aであるならば、Bである ] の逆は、[ Bであるならば、Aである ]です。
元の命題が真(正しいこと)であっても、その逆が真であるとは限りません。
【裏】
命題 [ Aであるならば、Bである ] の裏は、[ Aでないならば、Bでない ] です。
元の命題が真であっても、その裏が真であるとは限りません。
【対偶】
命題 [ Aであるならば、Bである ] の対偶は、[ Bでないならば、Aでない ] です。
元の命題が真であれば、その対偶も必ず真です。
【三段論法】
命題 [ Aであるならば、Bである ]、[ Bであるならば、Cである ] が共に真であるとき、[ Aであるならば、Cである ] も真です。
(1) 単純な命題問題・・・例題1
問題として与えられた命題が1つしかないときは、対偶について考えると、即答できるものが多いです。
(2) 複雑な命題問題・・・例題2
問題として与えられた命題が複数あるときは、三段論法を利用して解きます。
また、対偶と三段論法をどちらも使う複雑な問題も出題されます。
![]()
<基本問題>
「国語が好きな人は、算数が好きではない」という命題が正しいとき、確実に言えることは次のうちどれか。
- A算数が好きではない人は、国語が好きである
- B国語と算数が両方とも好きな人もいる
- C国語が好きではない人は、算数が好きである
- D算数が好きな人は、国語が好きではない
- E算数が好きな人の中には、国語が好きな人もいる
下図は、例題の命題の逆、裏、対偶の関係図である。
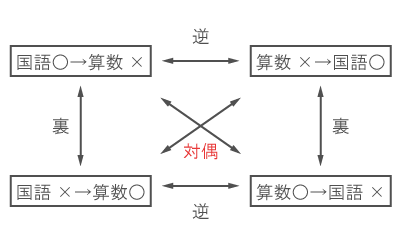
元の命題が真(正しいこと)であるとき、逆、裏は真であるとは限らないが、対偶は必ず真となる。
このような単純な命題問題では、問題として与えられた命題の対偶について考えると、即答できるものが多い。
「国語が好きな人は、算数が好きではない」の対偶は、「算数が好きな人は、国語が好きではない」となるため、Dが答えとなる。
他の選択肢の真偽は下記の通りとなる。
- A元の命題の逆 → 真とは限らない
- B元の命題と矛盾 → 偽
- C元の命題の裏 → 真とは限らない
- E対偶と矛盾 → 偽
「健康である人は、早寝早起きである」「スポーツができる人は、健康である」の2つが分かっているとき、次のアとイの真偽について正しく述べているものはどれか。
- ア早寝早起きである人は、健康である
- イスポーツができる人は、早寝早起きである
- Aアとイのどちらも必ず正しい
- Bアは必ず正しいが、イは正しいとは限らない
- Cアは必ず正しいが、イは必ず誤り
- Dアは正しいとは限らないが、イは必ず正しい
- Eアとイのどちらも正しいとは限らない
- Fアは正しいとは限らないが、イは必ず誤り
- Gアは必ず誤りだが、イは必ず正しい
- Hアは必ず誤りだが、イは正しいとは限らない
アの「早寝早起きである人は、健康である」は、問題文の「健康である人は、早寝早起きである」の逆のため、正しいとは限らない。
また、問題文の「健康である人は、早寝早起きである」「スポーツができる人は、健康である」の2つの命題を三段論法を使って図式化すると、下図のようになる。

そのため「スポーツができる人は、早寝早起きである」と言える。よって、イは必ず正しい。
これらを満たす選択肢は D である。
対偶
「タバコを吸わない人は、健康である」という命題が正しいとき、次のうち確実にいえるのはどれか。
| A健康な人は、タバコを吸わない |
| B健康でない人は、タバコを吸う |
| Cタバコを吸う人は、健康でない |
| D健康でない人は、タバコを吸うとは限らない |
| Eタバコを吸わない人でも、健康でない人がいる |
このような単純な命題問題では、問題として与えられた命題の対偶について考えると、即答できるものが多い。
問題として与えられた命題の対偶について考えると、選択肢Bの「健康でない人は、タバコを吸う」と一致する。
したがって、正解はBである。
他の選択肢の真偽は下記の通りとなる。
- A元の命題の逆 → 真とは限らない
- C元の命題の裏 → 真とは限らない
- D対偶と矛盾 → 偽
- E元の命題と矛盾 → 偽
三段論法
アとイの命題が正しいとき、次のうち確実にいえるのはどれか。
- ア動物であるならば、命がある
- イ人間であるならば、動物である
| A人間であるならば、命がある |
| B命があるならば、人間である |
| C動物であるならば、人間である |
| D人間でないならば、命がない |
| E人間でないならば、動物でない |
アとイの命題を三段論法を使って図式化すると下図のようになる。

よって、「人間であるならば、命がある」と言える。
したがって、答えはAとなる。
他の選択肢の真偽は下記の通りとなる。
- Bアの逆とイの逆を組合せたもの → 真とは限らない
- Cイの逆 → 真とは限らない
- Dアの裏とイの裏を組合せたもの → 真とは限らない
- Eイの裏 → 真とは限らない
対偶と三段論法
「肉が好きな人は、野菜が好きではない」「肉が好きではない人は、果物が好きではない」の2つが分かっているとき、次のアとイの真偽について正しく述べているものはどれか。
- ア野菜が好きな人は、果物が好きではない
- イ肉と野菜が両方とも好きな人もいる
| Aアとイのどちらも必ず正しい |
| Bアは必ず正しいが、イは正しいとは限らない |
| Cアは必ず正しいが、イは必ず誤り |
| Dアは正しいとは限らないが、イは必ず正しい |
| Eアとイのどちらも正しいとは限らない |
| Fアは正しいとは限らないが、イは必ず誤り |
| Gアは必ず誤りだが、イは必ず正しい |
| Hアは必ず誤りだが、イは正しいとは限らない |
対偶と三段論法を組合せて解く問題である。
「肉が好きな人は、野菜が好きではない」の対偶は、「野菜が好きな人は、肉が好きではない」となる。
この対偶と、「肉が好きではない人は、果物が好きではない」の2つを三段論法を使って図式化すると、次のようになる。

したがって、「野菜が好きな人は、果物が好きではない」と言えるため、アは必ず正しい。
イは、問題文の命題「肉が好きな人は、野菜が好きではない」と矛盾する。よって、必ず誤り。
これらを満たす選択肢は C である。
集合
ある会社の中でアとイのことが分かっている。確実にいえるのはどれか。
- ア1年目の社員はプログラマーである
- イ2年目の社員の中にもプログラマーはいる
| Aプログラマーであり1年目ではない社員は、2年目の社員である |
| Bプログラマーであり2年目ではない社員は、1年目の社員である |
| Cプログラマーは、1年目か2年目の社員である |
| Dプログラマーでない社員は、1年目の社員ではない |
| Eプログラマーでない社員は、2年目の社員である |
イに集合の概念が含まれているため、ベン図で条件を整理する。
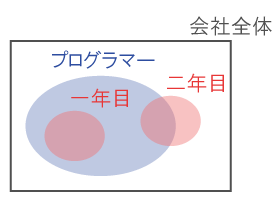
(※ 1年目、2年目の社員以外にも、社員がいるかもしれないことに注意して下さい。)
アの対偶である、Dの「プログラマーでない社員は、1年目の社員ではない」が正解となる。
また、ベン図から他の選択肢が誤りであることを確認できる。
