不等式と領域

＜ポイント＞

企業によっては線形計画法を業務で使うところもあります(ノ∀｀；)
・・・が、SPIには難しいものは出題されないので、ご安心を・・・(*´∀｀*)

中学で習った一次式、二次式のグラフを思い出しておけば十分です。

頻出の問題パターンは次の2つです。必ず押さえましょう。

（1）不等式が「一次関数」や「二次関数」などの数式で出題される問題・・・例題1

→ 「y >」ならグラフの「上」の領域！「y <」ならグラフの「下」の領域！

（2）不等式の条件が「文章」で出題される問題・・・例題2

→ それぞれの直線と縦軸、横軸が交差する点に注目しよう！

【出題されるグラフの種類】

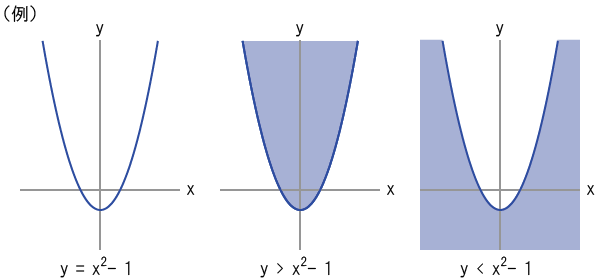
（1）「y = x2」系のグラフ

「y = x2」系の方程式によって表されるグラフは、下図の例のように放物線（上開き）である。
「y >」に置き換えると放物線の「上」の領域を表し、「y <」に置き換えると放物線の「下」の領域を表す。

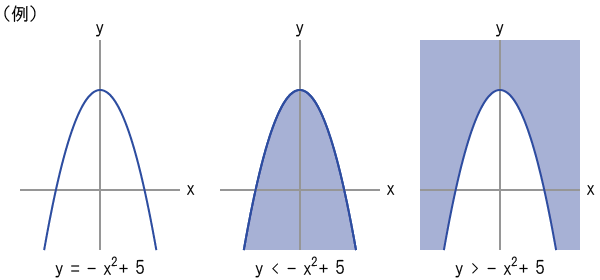
（2）「y = – x2」系のグラフ

「y = – x2」系の方程式によって表されるグラフは、下図の例のように放物線（下開き）である。
「y >」に置き換えると放物線の「上」の領域を表し、「y <」に置き換えると放物線の「下」の領域を表す

（3）「y = x」系のグラフ

「y = x」系の方程式によって表されるグラフは、下図の例のように直線（斜め・右上）である。
「y >」に置き換えると直線の「上」の領域を表し、「y <」に置き換えると直線の「下」の領域を表す

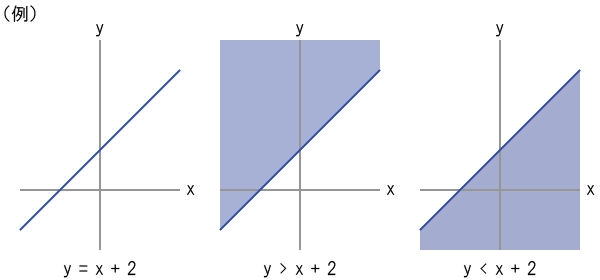
（4）「y = – x」系のグラフ

「y = – x」系の方程式によって表されるグラフは、下図の例のように直線（斜め・左上）である。
「y >」に置き換えると直線の「上」の領域を表し、「y <」に置き換えると直線の「下」の領域を表す。

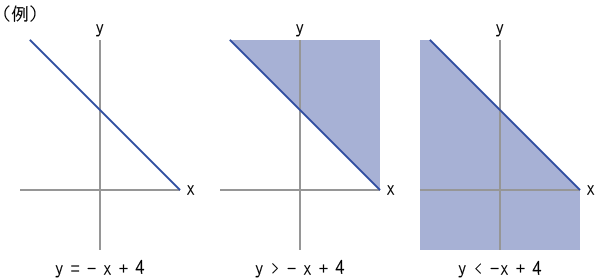
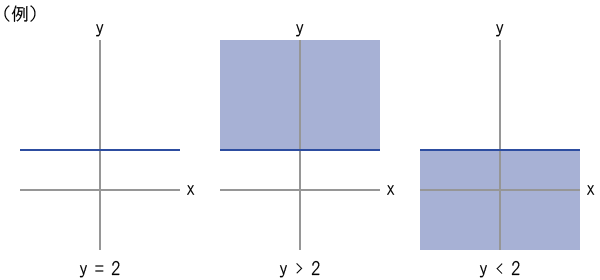
（5）「y = A」系のグラフ

「y = A」系の方程式によって表されるグラフは、下図の例のように直線（横）である。
「y >」に置き換えると直線の「上」の領域を表し、「y <」に置き換えると直線の「下」の領域を表す。

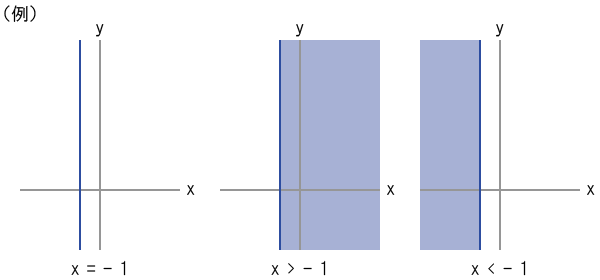
（6）「x = A」系のグラフ

「x = A」系の方程式によって表されるグラフは、下図の例のように直線（縦）である。
「x >」に置き換えると直線の「右」の領域を表し、「x <」に置き換えると直線の「左」の領域を表す。

 

 

＜基本問題＞

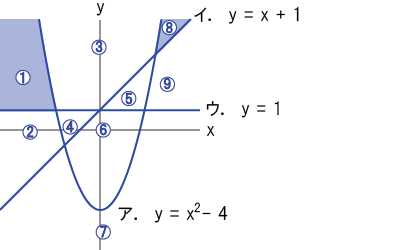
次の3つの式によって表される直線と放物線は、図のように平面を9つの領域に分ける。

  1. アy = x2 – 4
  2. イy = x + 1
  3. ウy = 1

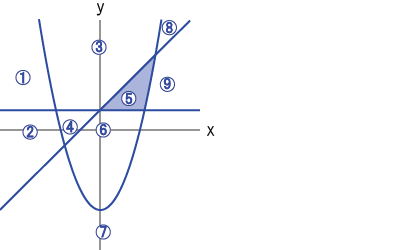
これらの領域は、上のア、イ、ウの各式の等号をそれぞれ不等号に置き換えた、1組の連立不等式によって表される。

  1. （1）ア、イ、ウの式の等号を、全て不等号に置き換えて、⑤の領域を表すとき、左開きの不等号（>）がつくのは、ア、イ、ウのうちどれか。
  1. Aアだけ
  2. Bイだけ
  3. Cウだけ
  4. Dアとイの両方
  5. Eアとウの両方
  6. Fイとウの両方
  7. Gアとイとウのすべて
  8. Hアとイとウのいずれにもつかない
  1. （2）次の連立不等式によって表される領域は、①から⑨のうちのどれか。
  1. アy < x2 – 4
  2. イy > x + 1
  3. ウy > 1
  1. A②
  2. B③
  3. C④
  4. D⑤
  5. E①と⑧
  6. F②と⑨
  7. G④と⑤
  8. HAからGのいずれでもない
（1）　E．アとウの両方

まず、ア、イ、ウの式がどのグラフを表すのかを考える。
ア．y = x2 – 4 → x2が式に含まれているため、放物線（上開き）のグラフ
イ．y = x + 1 → xが式に含まれているため、直線（斜め・右上）のグラフ
ウ．y = 1 → yが常に1なので、直線（横）のグラフ

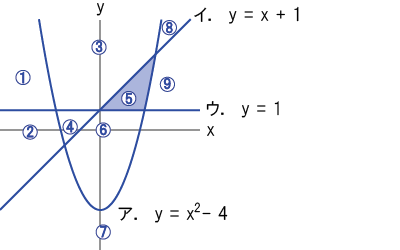
グラフの「上」の領域なら「y >」、グラフの「下」の領域なら「y <」になることに注意して、各式を不等号に置き換えよう。

⑤の領域は、アの「上」 → y > x2 – 4
⑤の領域は、イの「下」 → y < x + 1
⑤の領域は、ウの「上」 → y > 1

よって、左開きの不等号（>）がつくのはアとウの両方である。

（2）　E．①と⑧

ア．y < x2 – 4 → y = x2 – 4の「下」の領域
イ．y > x + 1 → y = x + 1の「上」の領域
ウ．y > 1 → y = 1の「上」の領域

よって、ア～ウの連立不等式によって表される領域は、下図の通り①と⑧である。

 

ある企業では、消耗品Pと消耗品Qを定期的に仕入れている。 Pの価格は1個当たり300円、Qの価格は1個当たり500円である。 1回に仕入れる量は、次の条件で決められている。

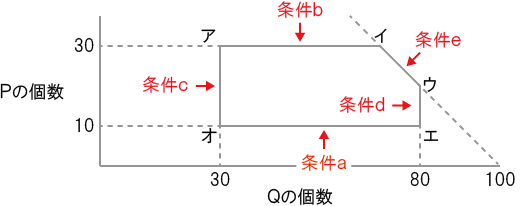
  1. 条件aPは10個以上であること
  2. 条件bPは30個以下であること
  3. 条件cQは30個以上であること
  4. 条件dQは80個以下であること
  5. 条件ePとQの合計が100個以下であること

これらの条件を満たす1回の仕入れ量は、図のア、イ、ウ、エ、オで囲まれた領域で表される。

 

  1. （1）点アと点イを通る直線で表される境界は、a～eのどの条件によるものか。
  1. A条件a
  2. B条件b
  3. C条件c
  4. D条件d
  5. E条件e
  1. （2）図の点のうち、最も値段が高い組合せを表すものはどれか。
  1. A点ア
  2. B点イ
  3. C点ウ
  4. D点エ
  5. E点オ
Ａ→（1）　B．条件b

それぞれの直線と縦軸、横軸が交差する点に注目する。

点アと点イを通る直線を延長すると、Pの個数を表す縦軸と交差する。 交差する点のPの個数は30個である。

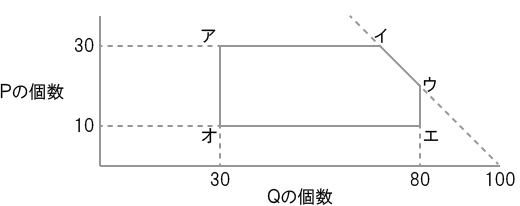
よって、この直線は条件b「Pは30個以下であること」によるものである。

Ａ→（2）　C．点ウ

最も値段が高い組合せを表す点の候補としては、 PとQをできる限り多く仕入れている、イとウが挙げられる。

条件e「PとQの合計が100個以下であること」より、イ、ウにおけるPとQの組合せは以下の通りであることが分かる。
イ → P：30個、Q：70個
ウ → P：20個、Q：80個

Pの価格は1個当たり300円、Qの価格は1個当たり500円なので、Qの個数が多いウが答えとなる。